Информатика и выч. техника \ Проектирование систем управления

Достижимость, минимальность, развязанные нули. Выходной развязанный нуль, ненаблюдаемость, хорошая сформированность, степень Макмиллана, биправильность, индекс управляемости, распределения, экспоненциальная устойчивость, правое/левое взаимно простое разложение, внутренняя правильность, страница 5

(а)

для называют экспоненциально устойчивым (exponentally stable), если для любых начальных значений и ее производных в величина стремится к нулю. Имеют место следующие свойства:

1) не включает распределения (distribution) при в форм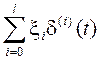е , где для всех i;

2) экспоненциально убывает, т. е. такое, что ограничено.

S99. экспоненциально устойчиво тогда и только тогда, когда , . (Эквивалентная формулировка: полиномиальная матрица D не имеет нулей в и в бесконечности тогда и только тогда, когда не имеет полюсов в и в бесконечности).

S100. Система экспоненциально устойчива (exponential stable) тогда и только тогда, когда справедливо:

1) любая траектория псевдосостояния при нулевом входе экспоненциально устойчива;

2) хорошо сформирована. Отметим, что 1) эквивалентно утверждению: такое, что

ограничено.

S101. экспоненциально устойчива тогда и только тогда, когда:

1) ;

2) правильные.

S102. Пусть экспоненциально устойчивая. Тогда:

1) при нулевом входе и экспоненциально затухают: т. е. такое, что и ограничены на ;

2) при любом управлении, кусочно дифференцируемом на , и при любых начальных условиях в предположении, что , справедливо:

i) если (u ограничено на ), то ;

ii) если , , то:

, ;

iii) если , то:

, .

S103. Передаточную функцию называют экспоненциально устойчивой (exponentially stable), если Н правильная и .

S104. Пусть - экспоненциально устойчивая, тогда:

1) и экспоненциально устойчивы тогда и только тогда, когда хорошо сформирована;

2) не имеет скрытых неустойчивых мод тогда и только тогда, когда не имеет развязанных нулей.

S105. , соответствующее , называют правым-левым взаимно простым разложением (right-left-coprime fraction), если:

1) ;

2) ;

3) справа взаимно простое, слева взаимно простое.

Если не выполняется 3), то называют правым-левым разложением (right-left fraction) для Н.

S106. Справедливо:

1) пусть - правое-левое разложение Н, тогда:

;

2) пусть - правое-левое взаимно простое разложение, тогда:

;

3) пусть - правое-левое взаимно простое разложение, тогда:

Н экспоненциально устойчиво Û .

S107. Правое-левое взаимно простое разложение для Н называют внутренне правильным (internally proper), если

правильные.

S108. Тройка называется левым-правым взаимно простым разложением (left-right-coprime fraction), если:

1) ;

2) ;

3) слева взаимно простое, справа взаимно простое.

Если не выполняется 3), то называют левым-правым разложением (left-right fraction) для Н.

S109. Пусть левое-правое взаимно простое разложение для Н. Тогда:

нуль .

S110. Пусть невырожденная, тогда:

1) ;

2) тогда и только тогда, когда существуют унимодальные матрицы такие, что:

i) - строчно-столбцово приведенная со строчными степенями и столбцовыми степенями ;

ii) , .

В 1) - столбцово приведенная, - строчно приведенная, - биправильная.

S111. Пусть имеет правое-левое разложение , где . Тогда:

1) - внутренне правильное (или эквивалентно: - хорошо устроена), если и только если , где - биправильная, - столбцово приведенная, - строчно приведенная. Кроме того, , - правильные рациональные матрицы;