Достижимость, минимальность, развязанные нули. Выходной развязанный нуль, ненаблюдаемость, хорошая сформированность, степень Макмиллана, биправильность, индекс управляемости, распределения, экспоненциальная устойчивость, правое/левое взаимно простое разложение, внутренняя правильность, страница 2

Докажем утверждение в другую сторону. Пусть  для . Перейдем к изображениям в последнем уравнении. Это равносильно тому, что  такое, что

                                                                                                         (з)

Из условия следует, что  - взаимно простые слева. Отсюда существуют такие , что  Умножим справа на :  и обозначим  и  Получим  Умножим слева на L(s):

                                                                                                      (и)

Но из (з) следует . Подставим в (и):

где  - полиномиальный вектор, следовательно, мы нашли такой вектор управления u(t), что соответствующая ему траектория  при  совпадает с . Следовательно, x(t) достижима S64.

$19.  Показать, что  полиномиальный вектор (г) S65.

S66.  Дана система:

                           .                      (а)

Любая траектория псевдосостояния  при нулевом входе достижима тогда и только тогда, когда пара  взаимно простая слева.

          В противном случае $ решение , не являющееся решением  для . Физический смысл состоит в том, что некоторые траектории псевдосостояния не могут быть возбуждены каким-либо входом.

S67.   называют входным развязанным нулем (input-decoupling zero) системы (а) из S66, если и только если для всякого наибольшего общего делителя  пары матриц  имеет место .

S68.  Любая траектория псевдосостояния  системы (а) из S66 при нулевом входе достижима тогда и только тогда, когда D не имеет входных развязанных нулей.

$20.  Показать, что  входной развязанный нуль, если и только если

.

S69.  Дана система (а) S66. Траектория псевдосостояния  при нулевом входе называется ненаблюдаемой (unobservable), если и только если , . Это равносильно тому, что существует  такое, что

.

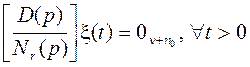          Комментарий. Если  - взаимно простые справа, то

.

S70.  Дана пара матриц , у которой наибольший общий правый делитель . Тогда существует  взаимно простые справа такие, что , . Взаимная простота  равносильна существованию  таких, что

                                                            ,                                                      (а)

и равносильна

                                                .                                            (б)

          Утверждение. Траектория  псевдосостояния  при нулевом входе тогда и только тогда ненаблюдаема, когда .

Доказательство. Пусть . Тогда  и , откуда  и . Следовательно,

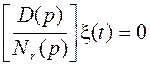                                                            ,                                                       (в)

т. е.  ненаблюдаемая (S69).

          Пусть  - ненаблюдаемая траектория. Тогда (S69) имеет место (в). перейдем к взаимно простым матрицам:  и умножим слева на : . Так как в левой части (до R) получаем единичную матрицу (а), доказали, что .

S71.  Дана система (а) из S66. Любая нетривиальная траектория псевдосостояния  при нулевом входе наблюдаема тогда и только тогда, когда  - взаимно простые справа.

Это динамическая интерпретация сокращения общих неунимодальных правых множителей в правом разложении  для .

S72.  z называют выходным развязанным нулем (output-decoupling zero) для системы (а) S66, если и только если для любого наибольшего общего правого делителя  пары  справедливо: .

S73.  Траектория псевдосостояния  при нулевом входе наблюдаема тогда и только тогда, когда нет выходных развязанных нулей.

Примечание. Система полностью наблюдаема тогда и только тогда, когда отсутствуют выходные развязанные нули.

$21.  Показать, что , тогда и только тогда, когда z - выходной развязанный нуль. Здесь матрица  имеет размеры .