Достижимость, минимальность, развязанные нули. Выходной развязанный нуль, ненаблюдаемость, хорошая сформированность, степень Макмиллана, биправильность, индекс управляемости, распределения, экспоненциальная устойчивость, правое/левое взаимно простое разложение, внутренняя правильность, страница 4

S89.  Система D имеет хорошо сформированное нулевое состояние тогда и только тогда, когда  и .

S90.  Система D хорошо сформирована (well formed), если для любых начальных условий вектора x и его производных и для любого входа  такого, что , имеем:  и .

S91.  Система  хорошо сформирована тогда и только тогда, когда матрицы

                                                                                                         (а)

правильные. Правильность матриц (а) равносильна , где Р системная матрица

.

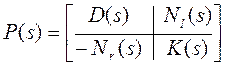S92.   называют приведенной по строчкам и столбцам (row-column-reduced), если и только если  такие, что

                                   ,                             (а)

где .  называют степенью i-й строки (row power),  называют степенью j-го столбца (column power),  называют коэффициентной матрицей при высших степенях (highest degree coefficient matrix). Матрицу D называют биправильной (biproper), если  и  правильные. Уравнение (а) эквивалентно:

                           ОКРУЖНАЯ         ,                                (б)

где  - биправильная,  - строчно приведенная,  - столбцово приведенная.

$23.  Найти связь между формулами (а) и (б) S92.

S93.  Пусть  - несингулярная приведенная по строчкам и столбцам. Обозначим элементы D через , т. е. . Следующие утверждения эквивалентны:

1)  D - приведенная по строчкам и столбцам с ,  - диагональная;

2)  .

$24.  Привести матрицу

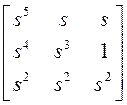
к виду, приведенному по строчкам и столбцам. Выполним несколько унимодальных операций. 1) Из первого столбца вычтем второй столбец, умноженный на s. Кратко это запишем так: . 2) К первому столбцу прибавим третий столбец, умноженный на : . 3) :

 ~  ~  ~ .

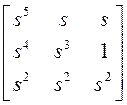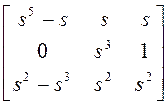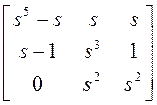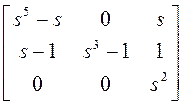Обозначим полученную матрицу через . Тогда .

S94.   приведенная по строчкам и столбцам тогда и только тогда, когда 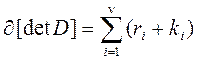. Здесь  - степени строк,  - степени столбцов.

S95.  Если  приведенная по строчкам и столбцам, тогда  - правильная.

Доказательство. Представим матрицу  так:

.

Матрица, стоящая в фигурных скобках, правильная: она равна  из (б) S92. Кроме того, последняя и первая матрицы также правильные. Следовательно, матрица  правильная.

$25.  Рассмотрим процедуру поиска (А, В, С) по строго правильной передаточной функции , если известно правое полиномиальное разложение  , т. е. . Обозначим . Числа  называют индексами управляемости (controllability indices) пары (А, В). введем матрицу

.

Оказывается, что

                                         .                                   (а)

Действительно,

.

Выражение в фигурных скобках получено из первой формулы (а). Из первой формулы (а) находим матрицы А, В и из второй - матрицу С.

S96.  Пусть  невырожденная приведенная по строчкам и столбцам, причем строчные степени  и столбцовые степени . Далее  такая, что ;  - такая, что . Тогда для всех i, j справедливы включения:

                                                         ,                                                      (а)

                                                          ,                                                      (б)

                                                        .                                                   (в)

          Докажем (а):

.

Матрицы, стоящие в фигурных скобках, правильные (см. доказательство в S95). Следовательно,  - правильная. Утверждение (а) доказано. Доказательство (б) и (в) совершенно аналогично и здесь не приводится.

S97.  Пусть дана система  такая, что D - приведенная по строчкам и столбцам, причем строчные степени  и столбцовые степени . Для всех  , , . Тогда  - хорошо устроенная.

S98.  Рассмотрим  невырожденную. Решение