Полиномиальные матрицы. Взаимно простые полиномы. Матрица Сильвестра. Взаимно простые полиномиальные матрицы. Строчное и столбцовое приведение полиномиальных матриц, страница 2

Множество полиномов не образуют поле, так как их обратные относительно умножения не являются полиномами. Если мы перейдем к расширенному множеству, включив наше множество во множество рациональных функций, то получим поле. Для матриц с элементами в поле  рациональных функций  понятия линейной независимости, ранга, и врожденности переносятся с матриц с элементами из поля вещественных или комплексных чисел. Таким образом, если мы будем рассматривать полиномы поля рациональных функций, то мы можем принять идеи линейной зависимости и ранга полиномиальных матриц.

Пусть A(s) полиномиальная матрица ранга r в поле рациональных функций ℝ(s). Посредством элементарных строчных операций она может быть приведена к виду

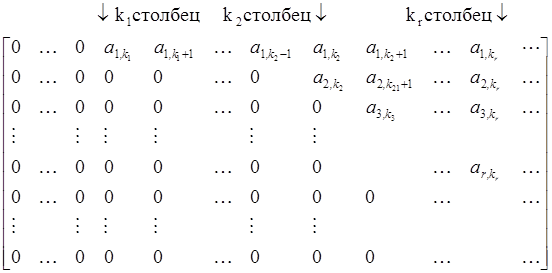
Первые rстрок ненулевые с полиномиальными элементами. Самый левый ненулевой элемент  каждой строки – нормированный полином. Элемент располагается правее элемента , т.е.  . При  получаем форму Смита. Степени всех элементов над меньше, чем степень , т.е. deg< deg, , . Если deg=0, тогда =0 для . Матрица с такими свойствами называется  строчной эрмитовой  (Hermit row form). В случае вещественных  элементов матрицы А, она оказывается строчной эшелонной формой (echelon row form). В этом случае самый левый ненулевой элемент в каждой строке равен единице.

Теорема 2.5. Любая полиномиальная матрица может быть приведена к эрмитовой строчной форме посредством последовательности элементарных строчных операций.

Определение 2.3. Квадратная полиномиальная матрица M(s) называется унимодальной матрицей (unimodular matrix), если ее детерминант не нуль и не зависит от s.

Теорема 2.6. Квадратная полиномиальная матрица унимодальная, если и только если ее обратная есть полиномиальная матрица.

Определение 2.4. Квадратная полиномиальная матрица R(s) есть наибольший общий правый делитель (greatest common right divisor) N(s) и D(s),если R(s) является общим правым делителем N(s) и D(s)  и левым кратным каждого общего правого делителя   N(s) и D(s). Если наибольший общий делитель является унимодальной матрицей, тогда N(s) и D(s) взаимно простыми справа (right coprime).

Теорема 2.7. Рассмотрим полиномиальные матрицы N(s) и D(s) размерами p*p и q*p. Тогда их наибольший общий правый делитель R(s) может быть выражен в формеR(s)=X(s)D(s) +Y(s)N(s), где X(s) и Y(s) полиномиальные матрицы p*p и q*p.

Следствие 2.3. Если  полного столбцового ранга, в частности  D(s) несингулярная, тогда все наибольшие общие делители N(s) и D(s) несингулярные  и связаны унимодальными матрицами.

Теорема 2.8. Пусть D(s) и N(s)  полиномиальные матрицы  размерами p*p и q*p, и пусть D(s) несингулярная. Тогда D(s) и N(s)  взаимно простые справа, если и только если имеет место  одно из условий:

1.Для любого s из ℂ или для каждого корня детерминанта D(s)матрица  размерами (p+q)*p имеет ранг p (в поле комплексных чисел).

2. Существуют полиномиальные матрицы X(s) и Y(s)порядка p*p и q*p такие, что X(s)D(s) +Y(s)N(s)=I. Это тождество называется тождеством Безу (Bezoue identicy).

3. Не существуют полиномиальные  матрицы B(s) и A(s) порядка q*p и q*q такие, что B(s)D(s) =A(s)N(s) или эквивалентно

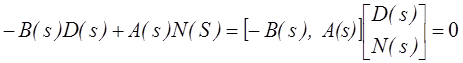
и deg det  A(s) < deg det D(s).

Теорема 2.9. Пусть A(s) и B(s) полиномиальные матрицы размерами q*q и q*p, и пусть A(s) несингулярная . Тогда A(s) и B(s) взаимно простые слева, если и только если имеет место одно из условий :

1. Для любого s из ℂ или для каждого корня детерминанта A(s) матрица  размерами q*(p+q) имеет ранг q (в поле  комплексных чисел).

2. Существуют полиномиальные матрицы и  порядка q*q и q*p такие, что .

3. Не существуют полиномиальные  матрицы N(s) и D(s) порядка q*p и p*p такие, что A(s)N(s)=B(s)D(s) или эквивалентно

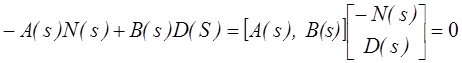
и deg det  D(s) < deg det А(s).