Информатика и выч. техника \ Проектирование систем управления

Полиномиальные матрицы. Взаимно простые полиномы. Матрица Сильвестра. Взаимно простые полиномиальные матрицы. Строчное и столбцовое приведение полиномиальных матриц, страница 3

Следствие 2.4. Пусть D(s) и N(s) – полиномиальные матрицы размерами  p*p и q*p и пусть D(s) несингулярная. Пусть U(s)- унимодальная матрица такая, что

≜.

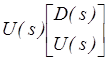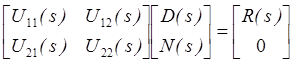Тогда

1)  U22(s) и U21(s) взаимно простые слева;

2)  U22(s) несингулярная и ;

3)  D(s) и N(s)взаимно простые справа, если и только если

deg det  D(s) = deg det U22(s)  .

2.3. Строчное и столбцовое приведение полиномиальных матриц

Рациональная функция g(s) называется строго правильной  (stri ctly proper), если g(∞) < ∞. Рациональная матрица G(s) правильная  если  и только если степень числителя каждого элемента матрицы G(s) меньше или равна степени знаменателя этого же элемента.

Теорема 2.10. Если G(s) q*p правильная (строго правильная) рациональная матрица и если , тогда

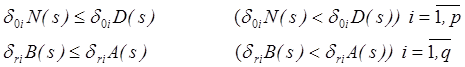
Пусть ,где . Матрицу из коэффициентов Mh0 называют столбцово степенной коэффициентной матрицей (column-degree coefficient matrix).

Матрица M(s) столбцово приведенная, если и только если ее столбцово степенная коэффициентная матрица Mh0 несингулярная .

Матрица M(s) может быть записана как , где . Матрицу из коэффициентов  Mhr называют строчно степенной коэффициентной матрицей (row-degree coefficient matrix).

Матрица M(s) строчно приведенная, если и только если ее строчно степенная коэффициентная матрица M несингулярная.

Теорема 2.11. Пусть N(s) и D(s) q*p и p*p полиномиальные матрицы и пусть D(s) столбцово приведенная. Тогда рациональная функция  правильная (строго правильная), Если и только если  

Теорема 2.12. Для каждой несингулярной полиномиальной  M(s) существуют унимодальные матрицы U(s) и V(s) такие, что M(s)U(s) и V(s)M(s) столбцово приведенная матрица  или строчно приведенная.

Теорема 2.13. Пусть N(s) и D(s) q*p и p*p полиномиальные матрицы и пустьD(s) несингулярная. Тогда существуют единственные q*p полиномиальные матрицы Q(s) и R(s) такие, что N(s)= Q(s)D(s)+R(s) и  строго правильная. Последнее утверждение может быть заменено , если D(s) столбцово приведенная.

Теорема 2.14. Пусть A(s) и B(s) полиномиальные матрицы размерами q*q и q*p, и пусть A(s) несингулярная. Тогда существуют единственные q*pполиномиальные матрицы Q(s) и R(s) такие, что B(s)= A(s)Q(s)+R(s) и  строго правильная. Последнее утверждение может быть заменено  если A(s) столбцово приведенная.

Следствие 2.15. Пусть D(s)=sI-A и N(s) произвольная полиномиальная матрица. Тогда существуют единственные Qr(s) и Q1(s) такие, что

2.4. Взаимно простое разложение правильных рациональных матриц

Теорема 2.15. Рассмотрим q*p правильную рациональную матрицу G(s) с правым взаимно простым разложением . Тогда для любого другого разложения  существует p*p невырожденная полиномиальная матрица T(s) такая, что

Если разложение  взаимно простые справа, тоT(s) унимодальная матрица.

Рассмотрим p*q правильную рациональную матрицу G(s). Пусть , где A(s), B(s), N(s) и D(s) полиномиальные матрицы размерами q*q, q*p, q*p, p*p соответственно. Уравнение  может быть записано в виде

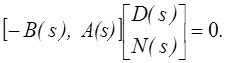                                   (2.10)

Если будем рассматривать полиномы как элементы поля вещественных рациональных функций ℝ (s), то это уравнение есть однородное линейное алгебраическое уравнение. Далее, все 1*(p+q) векторы x(s) с элементами в ℝ (s) (включающем полиномы), удовлетворяющие

,

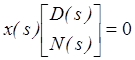образуют линейное пространство над ℝ (s). которое обозначим как (,ℝ(s)). Это пространство в (ℝp+q(s),ℝ (s)). Назовем его левым ядром (left null space). Его размерность равна

Скачать файл