Полиномиальные матрицы. Взаимно простые полиномы. Матрица Сильвестра. Взаимно простые полиномиальные матрицы. Строчное и столбцовое приведение полиномиальных матриц, страница 4

Полиномиальные решения называют полиномиальной частью и обозначают Множество q векторов в  называют полиномиальным базисом  (polynomial basis), если каждый вектор в может быть выражен единственным образом как комбинация q векторов с использованием полиномов в качестве коэффициентов. Отметим, что A(s) и B(s) слева взаимно простые, если и только если каждая из q строк  являются  базисными. Базис с наименьшими возможными степенями называется  минимальным полиномиальным базисом (minimal polynomial basis). Множество строк  является минимальным полиномиальным базисом, если и только если A(s) и B(s) слева взаимно простые и строчно приведенные.

Перепишем (2.10) в виде уравнения с вещественными коэффициентами. Для этого введем обозначения:

D(s)=D₀+D₁s+…+D_ds^d,                  N(s)=N₀+N₁s+…+N_ds^d,         (2.11)

A(s)=A₀+A₁s+…+A_ms^m,                 B(s)=B₀+B₁s+…+B_ms^m, где D_i, N_i,  A_i   и  В_i матрицы с вещественными коэффициентами. Подставим (2.11) в (2.10) и приравняем коэффициентами при sⁱ нулю. Получим систему уравнений

где

    (2.12)

Строки, сформированные из D_i назовем D строками, а из N_i – N строками. Матрица S_k имеет k+1 блочных строк. Каждая блочная строка имеет pD строк и qN строк. Находим линейно независимые строки сверху вниз. Обозначим через r₀ число линейно независимых строк в Nстроках первой блочной строки и т. д.

Лемма 2.1. Если  правильная, то все D строки в S_k к=1, 2, … линейно независимы.

Линейно зависимые строки, если их искать сверху вниз, находятся лишь N в строках.

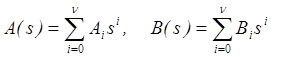Теорема 2.16. Рассмотрим q*p правильную рациональную матрицу , Сформируем S_k и найдем  ее линейно зависимые строчки, используя строчно- поисковый алгоритм. Пусть  будут q строк из K в , соответствующие первым q зависимым строкам из . Тогда полиномиальные матрицы  взаимно простые слева, и A(s) представлена в канонической форме, называемой полиномиальной эшелонной формой (polynomial echelon form).

Дадим пример такой формы:

.

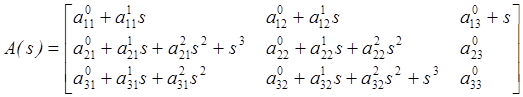Ведущие элементы обведены штриховой линией. Степень ведущего элемента больше степени каждого элемента правее в этой же строке  больше или равна степни каждого элемента левее в этой же строк.

Пример 2.2. рассмотрим обьект

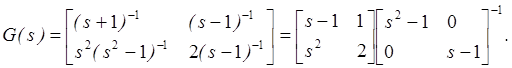
Это разложение невзаимно простое справа. Сформируем S₂ и применим строчный поисковой алгоритм: . Здесь

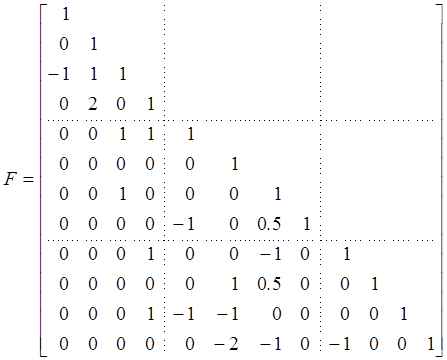
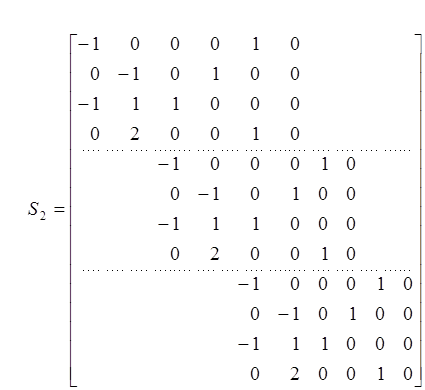
Первые зависимые строки помечены стрелками. В соответствии с этими первыми зависимыми стоками по (1.9) вычисляем:

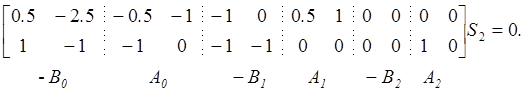
Решение получено в эшелонной форме. Тогда

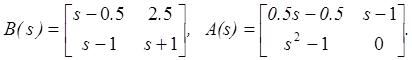
Отметим, что  и degdetA(s) равен общему числу линейно независимых N строк в S₂, A(s) и B(s) взаимно простые слева, и A(s) имеет полиномиальную эшелонную форму.

Следствие 2.5. Рассмотрим правильную рациональную матрицу G(s). Разложение  будет правым взаимно простым, если и только если degdetD(s)=n, где n- общее число линейно зависимых N строк в  или S_k для .

Лемма 2.2. m*m полиномиальная матрица T(s)=T₀+T₁s+…+T_js^j несингулярная (в поле рациональных функций), если и только если числовая матрица

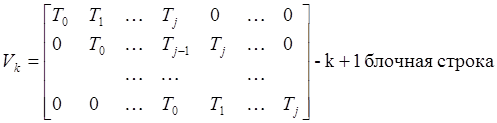
имеет полный строчный ранг (в поле комплексных чисел) для к=0, 1, …  .

Теорема 2.17. Пусть  будет левым взаимно простым разложением, и A(s) строчно приведенная. Тогда строчные степени A(s) являются внутренним свойством G(s) и не зависят от N(s) и D(s), упоминаемых в теореме 14 при вычислениях.

2.5. Неприводимость, управляемость, наблюдаемость и эквивалентность

Множество строчных индексов равно множеству степеней. Если  левое и правое взаимно простые разложения и A(s) строчно приведенное. Тогда множество строчных степеней A(s) единственно. Все решения x(s)

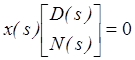
образуют q- мерное левое ядро. Множество q-строк  образуют полиномиальный базис левого ядра. Ввиду линейной зависимости строк S_k  найденных в порядке сверху вниз, строчные степени  наименьшие из возможных.