Полиномиальные матрицы. Взаимно простые полиномы. Матрица Сильвестра. Взаимно простые полиномиальные матрицы. Строчное и столбцовое приведение полиномиальных матриц, страница 5

Правильность обеспечивает и что все ведущие элементы появятся в A(s). Таким образом, строчные степени  равны  соответствующим строчным степеням A(s) , и A(s) строчно приведенная. Так как строчные степени A(s) наименьшие из возможных и так как множество строчных степеней единственно, множество q-строк  действительно образуют минимальный полиномиальный базис. Покажем, что если  и  слева взаимно простые, но  не строчно приведенная, тогда  не будет минимальным базисом. Действительно, так как и

Таким образом, строчные степени  не минимальные. Это доказывает, что  минимальный полиномиальный базис, если и только если A(s) и B(s) слева взаимно простые, и A(s)- строго приведенная.

Рассмотрим аналогично

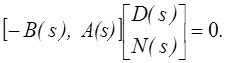
Все решения y(s) из  образуют p- мерное правое ядро. Если D(s) и N(s) взаимно простые справа, множество p- столбцов из  является полиномиальным базисом этого ядра. Дополнительно, если D(s) –столбцово приведенная, то это множество образует минимальный полиномиальный базис. Если решение получено с использованием столбцово  поискового алгоритма, тогда минимальный полиномиальный базис принимает эшелонную форму.

Определение 2.5. Характеристическим полиномом (characteristic polynomial) правильной рациональной матрицы G(s) называется наименьший общий знаменатель всех миноров G(s) . Степень G(s) (degree) определяется  как степень характеристического полинома G(s) и обозначается .

Возможны другие, но эквивалентные определения.

Определение 2.6. рассмотрим правильную рациональную матрицу G(s), представленную как разложения  Предположим, что N_r(s) и D_r(s) взаимно простые справа, а N₁(s) и D₁(s) взаимно простые слева. Тогда характеристический полином G(s) может быть определен  как det D₁(s) или det D_r(s), а степень G(s) как

Deg G(s)= deg det D₁(s) = deg det D_r(s)

Теорема 2.18. Управляемая реализация  наблюдаемая, если и только если D(s) и N(s) взаимно простые справа.

Теорема 2.19. Множество индексов управляемости любой несократимой реализации строго правильной рациональной матрицы G(s) равно множеству столбцовых степеней D(s) в любом столбцово приведенном взаимно простом правом разложении .

Определение 2.7. Полиномиальное матричное описание

                      (2.13)

где P(S), Q(s), R(s) и W(s) полиномиальные матрицы размером m*m, m*p, q*m и q*p, u(s) - вектор входа p*1, - псевдовектор состояния (pseudostate) m*1, y(s) – вектор выхода, называют неприводимым, если и только если P(s) и Q(s) взаимно простые справа.

Теорема 2.20. Рассмотрим полиномиальное матричное описание (2.13) с  n= degdetP(s).Тогда n – мерная динамическая  эквивалентная реализация (2.13) неприводима или эквивалентно управляемая и наблюдаемая, если и только если (2.13) неприводимо.

Эквивалентная форма записи (2.12)

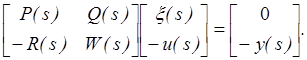
Матрица S(s)≜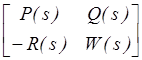 называется системной матрицей (system matrix).

 Определение 2.8. Две системные матрицы  S₁(s) и S₂(s) называются строго системно эквивалентными (strictly system equivalent), если и только если существуют m*m унимодальные полиномиальные матрицы U(s) и V(s) и  q*m и m*p полиномиальные матрицы X(s) и Y(s) такие, что

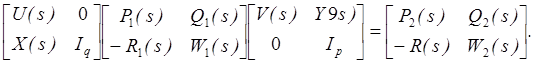
Теорема 2.21. Две системные матрицы строго системно эквивалентные имеют одну и ту же матричную передаточную функцию и detP₁(s)=kdetP₂(s), где kненулевая константа.

Теорема 2.22. Взаимная простота, управляемость и наблюдаемость инвариантны при преобразованиях, сохраняющих строго системную эквивалентность.

Теорема 2.23. Все неприводимые полиномиальные матричные описания , имеющие одну и ту же передаточную матрицу, строго системно эквивалентны.

Потребуем, чтобы выход системы отслеживал ступенчатое воздействие r(t)=r_d, приложенное к выходу системы. Если r_d =0, то эту задачу называют задачей регулирования (regulator problem). Если r_d ≠ 0, то эту задачу называют задачей асимптотического отслеживания (asymptotic tracking problem).

Рассмотрим p*p матрицу

Обозначим через

≜

где G_i(s) – i-строка матрицы W(s).

Теорема 2.24. Система с матричной передаточной функцией G(s) может быть развязана при помощи обратной связи по состоянию u=Kx+Hr, если и только если числовая матрица

несингулярная.