В нашем случае можно принять передаточное число равным 1, т.к. номинальные скорости вращения насоса и двигателя различаются всего на 1.3 процента. Следовательно статический момент механизма будет равен статическому моменту на валу двигателя.
Суммарный момент инерции электропривода определяется следующим образом:
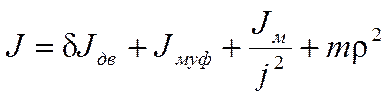 (9)
(9)
где: δ=1,15÷1,3 – коэффициент, учитывающий момент инерции вращающихся масс передаточного механизма;
Jдв – момент инерции ротора двигателя;
Jмуф – момент инерции соединительной муфты, тормоза и других частей механизма, непосредственно связанных с валом двигателя;
Jм – момент инерции вращающихся частей механизма;
j – передаточное число редуктора;
m – масса поступательно движущихся частей механизма, кг;
ρ – радиус приведения.
Примем суммарный момент инерции двигателя, равным трем моментам инерции двигателя, тогда:
![]() кг*м²
кг*м²
Основное уравнение движения ЭП:
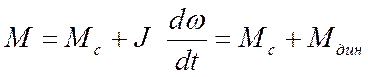 (10)
(10)
где: Мс – статический момент на валу двигателя;
Мдин – динамический момент электропривода;
J – суммарный момент инерции электропривода, кг·м².
Динамический момент электропривода Мдин определяют предварительно приближенно, принимая линейным закон изменения скорости, т.е.:
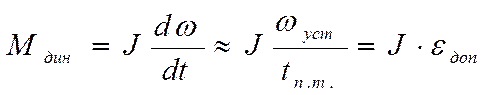 (11)
(11)
где: ωуст – установившаяся скорость двигателя на данном участке скоростной диаграммы, рад/с;
tп.т. – время пуска (торможения), с;
εдоп – допустимое угловое ускорение (замедление), рад/с.
Допустимое ускорение рассчитываем по следующей формуле:
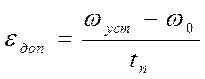 (12)
(12)
Примем время пуска от неподвижного положения до номинальной скорости равным времени торможения и равным 2с. Тогда допустимое ускорение по формуле (12) будет равно 153.8 рад/с². Рассчитываем динамические моменты и время переходного процесса (торможения или разгона) для всех режимов механизма, принимая линейным закон изменения скорости вращения механизма:
![]() Н*м.
Н*м.
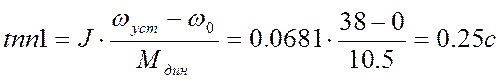
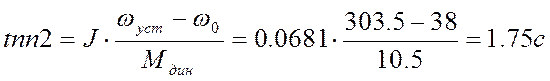
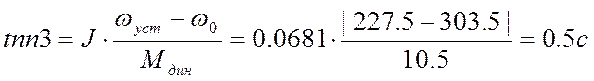
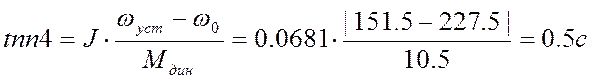
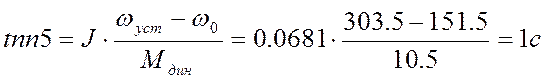
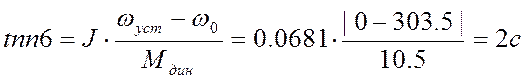
Зная времена переходных процессов и динамический момента, построим приближенную нагрузочную и скоростную диаграммы (см. Приложение1).
Теперь проведем проверку двигателя по нагреву с помощью метода эквивалентного момента. Условием правильного выбора двигателя будет:
![]() (13)
(13)
где:
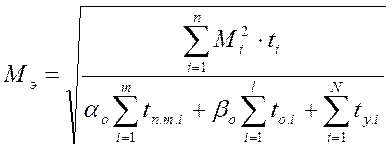 (14)
(14)
где: Мi – момент двигателя на i-ом интервале;
tо.i – продолжительность i-ой паузы;
tn.m.i – продолжительность пуска (торможения) на i-ом интервале;
tу.i – продолжительность установившегося движения на i-ом интервале;
l – количество пауз;
m – число интервалов пуска и торможения;
n – число рабочих интервалов в цикле;
N – количество интервалов установившегося движения;
αо – коэффициент ухудщения условий охлаждения при пуске, торможении двигателя с самовентиляцией (αо≈0,75 для двигателей постоянного тока; αо≈0,5 для асинхронных двигателей);
βо – коэффициент, учитывающий ухудшение охлаждения самовинтелируемого двигателя при отключении (βо=0,5 для закрытых двигателей и βо=0,3 для защищенных).
Рассчитаем эквивалентный момент в MathLab. При этом:
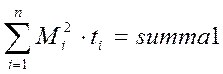 ;
; 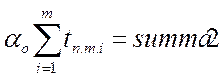 ;
; 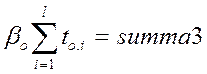 ;
;
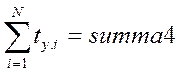 .
.
«задаем моменты на каждом интервале работы»
Mi=[3.05 28.98 17.46 9.22 28.99];
«продолжительность работы на каждом интервале в часах»
ti=[6 2 5 4 3]
ti1=ti*3600
summa1=0
for i=1:(length(Mi))
summa1=Mi(i)^2*ti1(i)
end
summa1 =9.0765e+006
a0=0.5
«длительности переходных режимов ЭП в секундах»
tpusk=[0.25 1.75 0.5 0.5 1 2]
summa2=sum(tpusk*a0)
summa2 =3
b0=0.5
«длительность пауз в часах»
tpauz=[3]
tpauz1=tpauz*3600
summa3=b0*tpauz1
summa3 =5400
summa4=sum(ti1)
summa4 =72000
«эквивалентный момент»
Mekw=sqrt(summa1/(summa2+summa3+summa4))
Mekw =10.8288
Таким образом видно, что эквивалентный момент Mekw =10.8288 Н*м меньше номинального Мном=36.2Н*м.
По приближенной нагрузочной диаграмме двигатель также проверяется и по перегрузочной способности в соответствии с условием:
![]() (15)
(15)
где: Мс.мах – максимальное значение статического момента на валу двигателя;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.