Теория машин и механизмов: Методические указания по выполнению контрольной работы

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

                  Федеральное агентство по образованию

Санкт-Петербургский государственный университет сервиса и экономики

Кафедра «Бытовые машины и приборы»

В.И. Полянский

Теория машин и механизмов

Методические указания
по выполнению контрольной работы для студентов специальностей 190603.65 (230100.02) «Сервис транспортных и технологических машин и оборудования (автомобильный транспорт)», 150408.65 (230300) «Бытовые машины и приборы», 260902.65 (280900) «Конструирование швейных изделий»

Санкт-Петербург

2006

Одобрены на заседании кафедры БМП, протокол №7 от 29.05.2001 г.

Утверждены Методическим Советом, протокол №9 от 27.06.2001 г.

Теория машин и механизмов. Методические указания по выполнению контрольной работы для студентов очного и заочного обучения специальностей 190603.65 (230100.02), 150408.65 (230300), 260902.65 (280900). – СПб.: Изд-во СПбГУСЭ, 2006. – 27 с.

Методические указания предназначены для выполнения контрольных работ № 1 «Кинематические исследования плоских механизмов» и № 2 «Кинематическое исследование планетарных зубчатых механизмов

Методические указания содержат все основные материалы, необходимые для выполнения контрольных заданий.

Составитель: к.т.н. В.И. Полянский

Рецензент: к.т.н., проф. В.В. Дыбок

Ó Санкт-Петербургский государственный университет сервиса и экономики

2006 г.

ВВЕДЕНИЕ

Теория механизмов и машин – наука об общих методах исследования свойств механизмов и машин и проектирования их схем.

Важнейшие задачи теории механизмов и машин – анализ механизмов, синтез механизмов и изложение теории машин. Анализ механизмов включает исследования кинематических и динамических свойств механизмов. При синтезе механизмов решаются задачи построения схем механизмов по заданным кинематическим и динамическим свойствам. При изложении теории машин рассматриваются вопросы механики.

По курсу «Теория механизмов и машин» для студентов специальности 2809, 2303, 2301 предусмотрено учебным планом выполнение контрольной работы на тему: «Кинематический анализ плоского кривошипно-шатунного механизма»

При выполнении этой контрольной работы необходимо руководствоваться требованиями ЕСКД / Единой системой конструкторской документации/ и соответствующих Гостов. Все вычисления должны быть проведены в системе СИ. Допускается использование технической системы измерений при условии перевода окончательных результатов в систему СИ.

Контрольная работа выполняется на обыкновенной писчей бумаге. Для замечаний рецензента требуется оставлять слева поля не менее 20 мм. Графические построения выполняются на миллиметровой бумаге карандашом в масштабе

1. Структурный анализ и кинематическое исследование плоских механизмов

Цель структурного анализа – определение степени подвижности и структурной формулы механизма (класса и порядка).

Из существующих методов кинематического исследования (анализа) механизмов: аналитического, графического, экспериментального и графо- аналитического – последний, благодаря своей простоте и наглядности, особенно для плоских механизмов, получил наибольшее распространение.

1.1. Структурный анализ

1.1.1. Степень подвижности

Степень подвижности (число степеней свободы) механизма определяет число звеньев с заданным законом движения, т.е. число входных звеньев механизма.

Степень подвижности плоских механизмов определяется по формуле П.Л. Чебышева:

W = 3n - 2p₅ - p₄,

где: n - число подвижных звеньев механизма;

       p₅ - число низших кинематических пар /пятого класса/;

       p₄ – число высших кинематических пар /четвертого класса/.

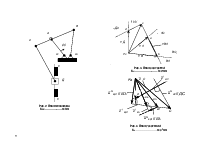
Пример: Определить степень подвижности механизма, изображенного на рисунке 1.

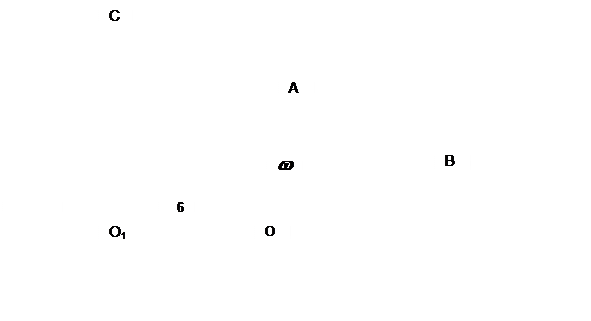
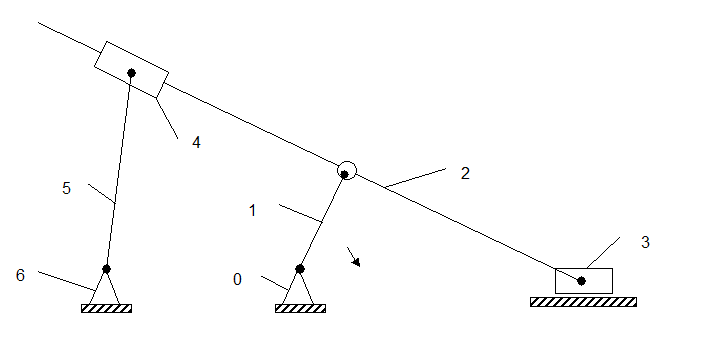
Рис. 1. Название звеньев:

звено 1 – кривошип; звено 2 – шатун; звено 3 – ползун;
звено 4 – камень кулисы; звено 5 – кулиса; звено 6 – стойка.

В этом механизме подвижными звеньями являются следующие:

1; 2; 3; 4; 5; т.е. n = 5

Число кинематических пар пятого класса будет:

6 – 1; 1 – 2; 2 – 3; 3 – 6; 2 – 4; 4 – 5; 5 – 6, т.е. p5 = 7

Число кинематических пар четвертого класса равно нулю, т.е. p₄ = 0.

Таким образом, имеем:

W = 3 5 – 2 7 – 0 = 1

Следовательно, степень подвижности механизма равна 1.

1.1.2. Определение класса и порядка механизма

Согласно классификации Ассуру – Артоболевскому всякий плоский механизм может быть образован из механизма (механизмов) первого класса путём наслоения на него (на них) структурных групп Ассура.

Входное звено, соединённое вращательное или поступательное парой со стойкой, называется механизмом первого класса.

Незамкнутая кинематическая цепь, которая при присоединении свободными элементами звеньев к стойке будет иметь нулевую степень подвижности, и не распадается на более простые цепи с нулевой степенью подвижности, называется группой Ассура. В группу Ассура входит только низшие кинематические пары.

W = 3п – 2Р₅ = 0

или 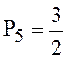                                                       п

Группы Ассура делятся на классы и порядки. Класс группы Ассура определяется высшим классом замкнутого контура, входящего в её состав. Контур – это звено или система звеньев.

Класс контура – число кинематических пар, образующих контур (табл. 1).

Таблица 1.

Номер класса контура

Порядок группы Ассура определяется числом внешних (свободных) элементов звеньев, которыми она присоединяется к механизму (табл. 2).

Состав и последовательность присоединения групп Ассура определяется формулой строения механизма.

Таблица 2.

Классификация структурных групп Ассура

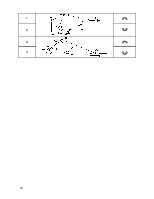
Рассмотрим пример выполнения классификации по группамАссура для механизма изображенного на рис. 1.

1. Выбираем входное звено, которое со стойкой образует кинематическую пару, т.е. звено 1. В данном случае имеем механизм  класса т.е.  или основной механизм.

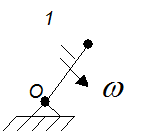
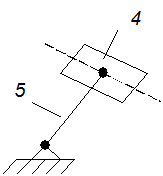
2. Отсоединяем наиболее удалённую от входного звена группу Ассура (на рис. 1 показана тонкой линией) со звеньями 4-5, которая, согласно табл. 1и2, является группой второго класса и второго порядка , состоящую из двух звеньев и трёх кинематических пар. Такая незамкнутая кинематическая цепь, будучи присоединённая свободным звеном 5 к стойке, будет иметь нулевую степень подвижности, т.е.:

W = 3п – 2Р₅ = 3·2 - 2·3 = 0

Оставшаяся часть кинематической цепи остаётся механизмом с прежней степенью свободы W = 1.

3. Отсоединим структурную группу Ассура со звеньями 2-3 (на рис. 1 показана тонкой линией),

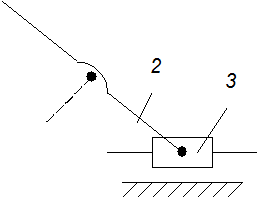
которая является второго класса и второго порядка . Подвижность механизма также будет равна нулю.

Составим последовательность присоединения групп Ассура и получим формулу строения механизма (рис)

В формуле строения римскими цифрами обозначены классы групп Ассура, а арабскими при римских цифрах – порядок группы. Цифрой  обозначен механизм первого класса.

1.2. Кинематическое исследование плоских механизмов

1.2.1. Построение кинематической схемы и плана положений механизма