Для определения ускорения точки В к вектору ускорения точки
А прибавляем вектор относительного нормального ускорения ![]() , направленный параллельно ВА.
Отложив величину этого вектора / влево от точки а /, проводим перпендикулярно
звену ВА линию действия вектора касательного ускорения
, направленный параллельно ВА.
Отложив величину этого вектора / влево от точки а /, проводим перпендикулярно
звену ВА линию действия вектора касательного ускорения ![]() .
Затем из полюса плана ускорения
.
Затем из полюса плана ускорения ![]() проводим линию,
параллельную ВО1 и на ней откладываем / вниз / величину вектора
нормального ускорения
проводим линию,
параллельную ВО1 и на ней откладываем / вниз / величину вектора
нормального ускорения ![]() . Через полученную точку
проводим перпендикулярно звену ВО1 линию действия вектора
касательного ускорения
. Через полученную точку
проводим перпендикулярно звену ВО1 линию действия вектора
касательного ускорения ![]() .
.
На пересечении линий действия векторов ![]() и
и ![]() находится
конец вектора абсолютного ускорения точки В. Отрезок
находится
конец вектора абсолютного ускорения точки В. Отрезок ![]() и
изображает этот вектор.
и
изображает этот вектор.
Ускорение точки С находим методом пособия. Соединив точки а и в на плане ускорений, получаем вектор полного относительного ускорения:
![]() .
.
Из пропорции 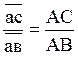 находим величину
отрезка
находим величину
отрезка ![]() :
:
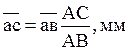
Откладываем этот отрезок на
продолжении отрезка ![]() находим точку с. Отрезок
находим точку с. Отрезок ![]() изображает вектор абсолютного
ускорения точки С.
изображает вектор абсолютного
ускорения точки С.
Для определения ускорения точки Д рассмотрим движение этой точки относительно точек С и Ду:
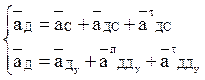
Величину отрезка, изображающего вектор нормального ускорения
![]() определяем расчетным путем:
определяем расчетным путем:
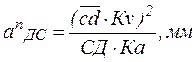
Направлен вектор ![]() параллельно шатуну
СД /от точки Д к точке С/, а вектор касательного ускорения
параллельно шатуну
СД /от точки Д к точке С/, а вектор касательного ускорения ![]() - перпендикулярно звену СД.
- перпендикулярно звену СД.
Ускорение точки Ду /точка не подвижна/ ![]() = 0 ; нормальное ускорение
= 0 ; нормальное ускорение ![]() также равно нулю, т. к. траектория
движения точки Д – прямая линия и радиус ее кривизны равен бесконечности:
также равно нулю, т. к. траектория
движения точки Д – прямая линия и радиус ее кривизны равен бесконечности:
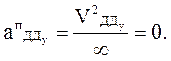
Касательные ускорение ![]() направлено
параллельно оси у-у.
направлено
параллельно оси у-у.
Для определения ускорения точки Д к вектору ускорения точки
С на плане ускорений прибавляем вектор относительного нормального ускорения ![]() направленный от Д к С /вверх/.
Отложив величину этого вектора, проводим перпендикулярно эвену СД линию
действия вектора касательного ускорения
направленный от Д к С /вверх/.
Отложив величину этого вектора, проводим перпендикулярно эвену СД линию
действия вектора касательного ускорения ![]() .
Затем из полюса плана
.
Затем из полюса плана ![]() проводим параллельно оси
у-у направляющих линию действия вектора
проводим параллельно оси
у-у направляющих линию действия вектора ![]() ;
на пересечении линий действия векторов
;
на пересечении линий действия векторов ![]() и
и
![]() находим конец вектора ускорения
точки Д. Отрезок
находим конец вектора ускорения
точки Д. Отрезок ![]() изображает вектор
абсолютного ускорения точки Д.
изображает вектор
абсолютного ускорения точки Д.
Абсолютные ускорения точек будет равны:
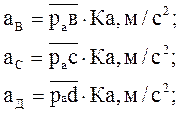
Дифференциальные и планетарные механизмы благодаря их преимуществ (малые габариты и большие величины u) по сравнению с рядовыми зубчатыми механизмами нашли широкое распространение в общем машиностроении.
Задание студента может содержать как дифференциальный, так и планетарный механизм. В связи с этим при определении подвижности механизма необходимо иметь введу что дифференциальный механизм имеет две степени подвижности (W=2), а планетарный – одну (W=1).
Пример:
Дан механизм, рис. 5 состоящий из ведущего центрального колеса Z1 = 80, водила Н, двойного сателита Z2 = 35 и Z3 = 25, одинарного сателита Z4 = 45 и ведомого центрального колеса Z5 = 160. Число оборотов водила Пн = 500 об/мин., первого колеса П1 = -300 об/мин., /знак “+” означает вращение по часовой стрелке, знак “-“ – против часовой стрелки/.
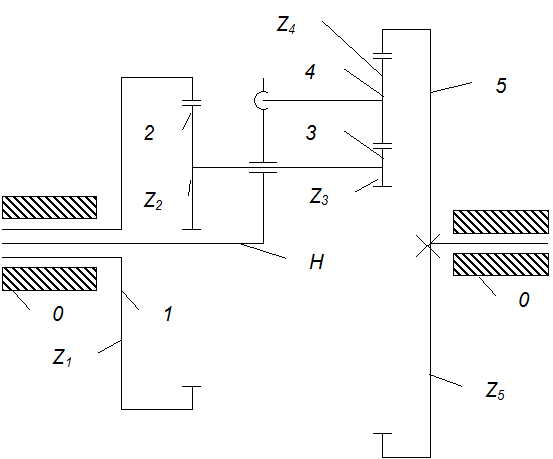
Рис. 5. Кинематический анализ механизма.
Механизм содержит:
Подвижные звенья: зубчатые колёса 1; (2-3); 4; 5; и водило H по этому n=5 число кинематических пар пятого класса P5=5 Соединение звеньев: (0-1; 0-H; H-(2-3); H-4; 5-0),а
Число кинематических пар P4=3 соединение звеньев 1-2; 4-3; 4-5
Следовательно, степень подвижности механизма будет:
![]()
т.е. ![]()
Таким образом, данный механизм является дифференциальным.
В случае планетарного механизма,
когда колесо 1 неподвижно т.е. ![]() =0
=0
Подвижных звеньев будет n=4, число кинематических пар пятого класса P5=4
(0-H; H-(2-3); H-4; 5-0), а число кинематических пар четвертого класса P4=3 в этом случае подвижность механизма составит:
![]()
![]()
Целью кинематического исследования планетарных механизмов является определение передаточных отношений и угловых скоростей звеньев. Эта задача может быть выполнена аналитическим, табличным и графо – аналитическим методами. При решении задачи № 2 в контрольной работе следует использовать аналитический метод. Аналитический метод исследования планетарных механизмов заключается в решении основного уравнения / формулы Виллиса /; когда к планетарному механизму применяется метод инвенсии таким образом, чтобы водило превратилось в стойку. Это возможно когда всему механизму условно сообщается вращение (-ωн), тогда водило становится неподвижным, а механизм превращается в обыкновенную передачу.
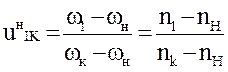
где: ![]() -
передаточное число от 1 –го /ведущего/ колеса к К – му /ведомому/, определяемое
как для простой зубчатой передачи /при неподвижном водиле/;
-
передаточное число от 1 –го /ведущего/ колеса к К – му /ведомому/, определяемое
как для простой зубчатой передачи /при неподвижном водиле/;
![]() -
угловая скорость ведущего центрального колеса /число оборотов /;
-
угловая скорость ведущего центрального колеса /число оборотов /;
![]() -
угловая скорость водила /число оборотов /;
-
угловая скорость водила /число оборотов /;
![]() -
угловая скорость ведомого колеса /число оборотов /.
-
угловая скорость ведомого колеса /число оборотов /.
В случае простого планетарного механизма, когда центральное
колесо неподвижно ![]() уравнение примет вид:
уравнение примет вид:
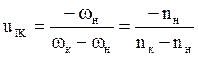
Рассмотренный выше (рис. 6) механизм является дифференциальным, по этому основное уравнение для него будет:
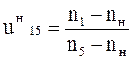
Передаточное число ![]() определяется
как для простой зубчатой передачи с учетом знаков передаточных чисел отдельных
пар колес /для внешнего зацепления « - », а для внутреннего “+”/:
определяется
как для простой зубчатой передачи с учетом знаков передаточных чисел отдельных
пар колес /для внешнего зацепления « - », а для внутреннего “+”/:
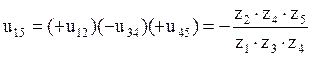
или
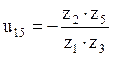
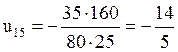
Подставляя значение передаточного числа в основное уравнение дифференциального механизма, получим:
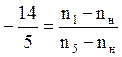 или
или 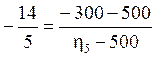
откуда ![]() об/мин.
об/мин.
Для определения числа оборотов колеса составляем следующее уравнение:
Где 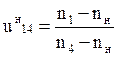
Тогда 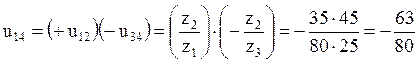
Откуда 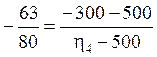
![]() = 1516 об/мин
= 1516 об/мин
Для определения числа оборотов блока сателлитов (Z2 –Z3) составляем уравнение:
Где 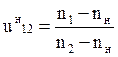
Тогда 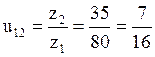
Откуда 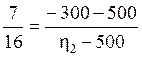
![]() об/мин.
об/мин.
Планетарное передаточное число равно отношению числа оборотов водила к числу оборотов ведомого колеса:
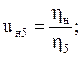
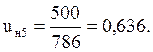
Выполнить кинематический анализ плоского механизма для
положения характеризующегося углом поворота кривошипа ![]() .
.
Угол отсчитывается от горизонтального положения кривошипа по часовой стрелке или против часовой – в зависимости от задания.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.