МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МЕХАНИКИ
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовому проекту по теории машин и механизмов
на тему: Анализ и синтез механизма вязального аппарата
Автор проекта
Специальность
Обозначение проекта
Группа
Руководитель проекта
Проект защищен
Члены комиссии
НОВОСИБИРСК, 2005
Введение
В данном курсовом проекте рассматриваются механизм вязального аппарата и планетарный редуктор. Целью проекта является изучение конструкции механизма его движения, под действием заданных сил. Курсовой проект состоит из четырех частей:
· структурный анализ,
· кинематический,
· силовой анализ,
· синтез планетарной передачи.
В первой части рассматривается механизм вязального аппарата. Для этого механизма проводится структурный анализ, определяется подвижность механизма и делается классификация всех его элементов по различным параметрам.
Во второй части проекта проводится кинематический анализ, заключающийся в нахождении зависимостей характеристик, описывающих его положение в конкретный момент времени и вычисление значений этих характеристик в двенадцати положениях механизма.
Третья часть работы посвящена определению сил, моментов, действующих на механизм и нахождению реакций возникающих в его конструкции под действием этих сил.
В четвертой части рассматривается зубчатый механизм, который называется планетарным редуктором. Для него по заданным геометрическим параметрам и техническим требованиям уточняется геометрия конструкции, и определяются значения некоторых его характеристик.
Раздел 1. Структурный анализ механизма вязального аппарата.
1.1. Структурный анализ.
1.1.1. Рисуем структурную схему механизма (рис. 1.1).

1.1.2. Выявляем сложные и разнесенные кинематические пары. В механизме вязального аппарата разнесенных кинематических пар не имеется, но есть сложная кинематическая пара B2, B3.
1.1.3. Классифицируем кинематические пары механизма (табл. 1.1).
Таблица 1.1
Классификация кинематических пар
|
№ п/п |
Номер звеньев, образующих пару |
Условное обозначение |
Название |
Подвиж-ность |
Высшая/ Низшая |
Замыка-ние (Геомет-рическое/Силовое) |
|
1 |
0-1 |
|
Враща-тельная |
1 |
Н |
Г |
|
2 |
1-2 |
|
Враща-тельная |
1 |
Н |
Г |
|
3 |
2-3 |
|
Посту-патель-ная |
1 |
Н |
Г |
|
4 |
3-0 |
|
Враща-тельная |
1 |
Н |
Г |
|
5 |
3-4 |
|
Враща-тельная |
1 |
Н |
Г |
|
6 |
4-5 |
|
Враща-тельная |
1 |
Н |
Г |
|
7 |
5-0 |
|
Враща-тельная |
1 |
Н |
Г |
Рассматриваемый механизм состоит только из одноподвижных кинематических пар (p1=7, p=7), где p1-числоодноподвижных кинематических пар, а p-обще число кинематических пар в механизме.
1.1.4. Классифицируем звенья механизма (табл. 1.2).
Таблица 1.2
Классификация звеньев
|
№ п/п |
Номер звена |
Условное обозначение |
Название |
Движение |
Число вершин (t) |
|
1 |
0 |
|
Стойка (0) |
Отсутствует |
- |
|
2 |
1 |
|
Кривошип (1) |
Вращательное |
2 |
|
3 |
2 |
|
Камень (2) |
Сложное |
2 |
|
4 |
3 |
|
Кулиса (3) |
Вращательное |
3 |
|
5 |
4 |
|
Шатун (4) |
Сложное |
2 |
|
6 |
5 |
|
Коромысло (5) |
Вращательное |
2 |
Данный механизм имеет: четыре простых звена – 1, 2, 4, 5; одно сложное звено – 3.
1.1.5. Находим число присоединений к стойке. Рассматриваемый механизм имеет три (S=3) присоединения к стойке.
1.1.6.Выделяем в сложном механизме структурные группы Ассура и элементарные механизмы. Проводим классификацию структурных групп. В данном механизме можно выделить один элементарный механизм (рис. 1.2)
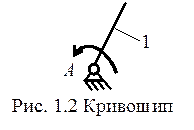
 и две структурные
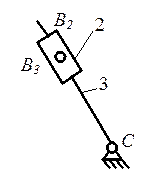
группы – Диады (рис. 1.3)
и две структурные
группы – Диады (рис. 1.3)
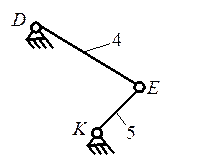
Рис. 1.3
Подвижность структурных групп определяется по следующей формуле
![]()
Как для первой, так и для второй структурной группы число звеньев равно двум (n=2), число одноподвижных кинематических пар равно трем (p1=3), двуподвижных кинематических пар здесь не имеется (p2=0), значит
![]()
Определим порядок и класс структурных групп. Первая структурная группа присоединяется к механизму с помощью двух звеньев – 5, 4, вторая с помощью звеньев 2 и 3, таким образом, порядок обоих структурных групп равен двум.
Класс у структурных групп определяется числом кинематических пар, которые образуют самый сложный замкнутый контур. У обеих структурных групп класс равен двум.
Раздел 2. Кинематический анализ механизма вязального аппарата.
2.1. Аналитический метод Зиновьева определения положений звеньев механизма.
2.1.1. Убеждаемся в том, что перед нами механизм (рис. 1.1). Воспользуемся формулой Чебышева и определим подвижность механизма
![]()
![]()
равенство выполнилось, значит перед нами механизм.
2.1.2. Выбираем ведущее звено. Ведущим звеном является звено 1, закон его движения задан. Ведомым звеном является звено 5.
2.1.3. Выбираем систему координат. Обычно начало системы координат помещают в стойку ведущего звена. Заменяем звенья механизма на вектора.


2.1.4. Образуем из векторов замкнутые контуры. При этом контуров может быть сколько угодно и вектора могут начинаться где угодно, но в контур должно входить не более двух неизвестных параметров. Составляем три замкнутых контура- ABCH, CDK, KDE.
2.1.5. Составляем векторные уравнения замкнутости контуров при их обходе по часовой стрелке.
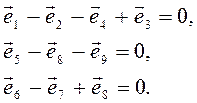
Делаем проекции полученных уравнений на оси и записываем три системы уравнений.
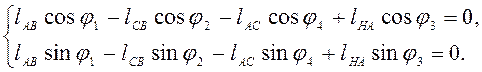 (2.1)
(2.1)
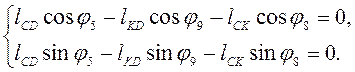 (2.2)
(2.2)
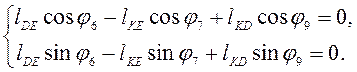 (2.3)
(2.3)
Решаем
систему (2.1) относительно ![]()
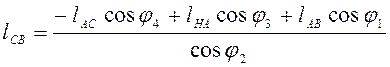
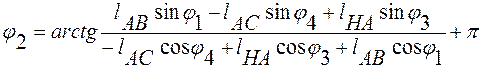
![]()
Решаем
систему (2.2) относительно ![]()
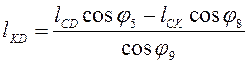
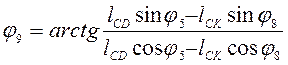
Решаем
систему (2.3) относительно ![]() .
.
Слагаемые с φ6 переносим в правые части уравнений, возводим их в квадрат и складываем
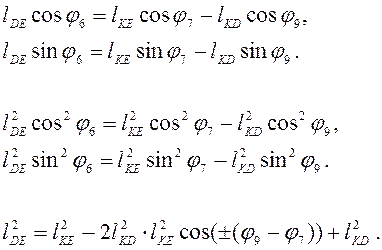
Пусть 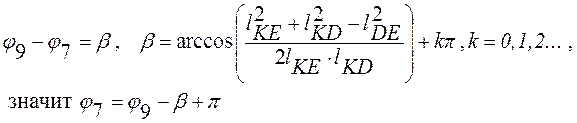
Для определения φ6 воспользуемся первым уравнением системы (2.3)
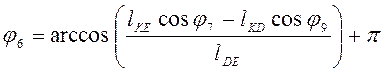 .
.
Решаем выше
представленные уравнения в MathCAD 11, учитывая, что ![]()
|
lAB, м |
0,18 |
|
lCD= lDE, м |
0,70 |
|
lKE, м |
0,28 |
|
x1=0,5y, м |
0,23 |
|
x2, м |
0,94 |
|
ωd, рад/с |
122 |
Результаты решения систем представлены в табл. 2.1.
Таблица 2.1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.