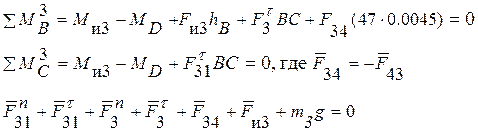
6. Рассматривая начальное звено, составляем уравнение моментов относительно точки в стойке, откуда определяем уравновешивающий момент M1.
![]()
7. Составляем уравнение равновесия всех сил, действующих на начальное звено, и определяем реакции в кинематической паре A.
![]()
При графическом построении векторов сил, векторами у которых длина менее 1 мм пренебрегаем.
После
рассмотрения структурной группы (см. рис.1.3(1)), получили ![]() , в положении 5, и
, в положении 5, и ![]() , в положение 10. Знак «минус»
указывает на то, что реальное направление реакции противоположно направлению,
обозначенному на схеме.
, в положение 10. Знак «минус»
указывает на то, что реальное направление реакции противоположно направлению,
обозначенному на схеме.
После
рассмотрения структурной группы (см. рис.1.3(2)), получили ![]() , в положении 5, и
, в положении 5, и ![]() , в положение 10.
, в положение 10.
После
рассмотрения начального звена (см. рис.1.2), получили ![]() ,
в положении 5, и
,
в положении 5, и ![]() , в положение 10.
, в положение 10.
Раздел 4. Синтез планетарной передачи.
4.1 Подбор числа зубьев колес и сателлитов механизма.
Исходные данные
Таблица 4.1.1
|
aω, мм |
66 |
|
z1 |
11 |
|
z2 |
30 |
|
m1, мм |
3 |
|
i53H |
4,5 |
|
m2, мм |
3,5 |
При конструировании планетарной ступени необходимо выполнение следующих условий:
1. условие соосности;
2. условие соседства;
3. условие сборки.
Помимо этого число зубьев колес с внутренним зацеплением должно превышать 85, а с внешним зацеплением – 17.
В соответствии с условиями получаем следующие уравнения:
Колеса 2, 3, 5 имеют общий центр, поэтому уравнение соосности имеет вид:
z5-z4=z3+z4 (4.1.1)
Уравнение соседства имеет вид:
![]() (4.1.2)
(4.1.2)
Уравнение сборки:
![]() (4.1.3)
(4.1.3)
Здесь z3, z4, z5-числа зубьев колёс , ![]() -число
сателлитов,c- целое число.
-число
сателлитов,c- целое число.
Передаточное отношение можно определить по формуле:
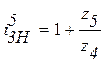 (4.1.4)
(4.1.4)
Передаточное отношение зубчатого механизма определяется по формуле:
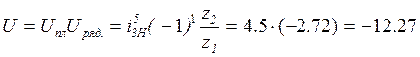 (4.1.5)
(4.1.5)
Решая данную систему уравнений, определяем число зубьев колес и число сателлитов.
В итоге выбираем наиболее удобный вариант:
|
k |
c |
z3 |
z5 |
z4 |
|
3 |
42 |
28 |
98 |
35 |
4.2 Построение планов линейных и угловых скоростей.
Находим
начальные диаметры колёс планетарной передачи и вычерчиваем кинематическую
схему механизма, приняв масштабный коэффициент ![]() 3,5
мм/мм
3,5
мм/мм
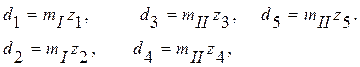
![]()
Учитывая масштабный коэффициент, получим:
![]()
1. Строим план линейных скоростей. (рис. 4.2.1)
Проводим прямую параллельно водилу механизма. Отмечаем все кинематические пары A, B, C, D, E, A’, O.
Из точки d откладываем вектор dd’, изображающий скорость точки D колеса 3 и 4. Соединив точку d’ с точкой О, получим линию 3 распределения линий скоростей колеса 3.
Для колеса 4 известны скорости двух точек: D и B =0. Прямая 4, соединяющая точки d’ и b, является линией распределения скоростей колеса 4. На этой линии лежит точка c’ - конец вектора cc’ ,изображающего скорость точки C ,общей для звеньев 4 и Н. Соединив точку c’ с точкой О, получим линию Н распределения скоростей звеньев Н-4.
Вектор ee’ есть скорость точки E колеса 1 и 2/
2. Строим план угловых скоростей.
Ниже точки О откладываем отрезок произвольной длины PP’. Из точки P' проводим прямые, параллельные линиям 3, 4, 1, Н до пересечения их в точках 3, 4, 1, Н с перпендикуляром к PP’.
Передаточное отношение планетарной передачи можно найти как отношение косинусов соответствующих углов:
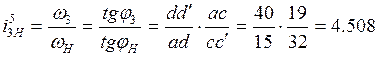
Сравнивая полученное значение с исходными данными, видно, что значения практически сходятся и погрешность равна 0.17%.
Передаточное отношение планетарной передачи определим аналогично:
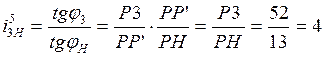

Заключение
В данном курсовом проекте произведено структурный, кинематический, силовой анализы механизма вязального аппарата и синтез планетарной передачи.
Все этапы проведения работы точно соответствуют поставленным алгоритмам решения данных задач. В результате выполнения проекта получены численные значения искомых характеристик, разобраны схема, элементы конструкции, проанализирована и уточнена геометрия механизмов, а также в масштабе выполнены чертежи заданных механизмов, отдельных их узлов и векторных характеристик.
Все расчеты были проведены с помощью пакетов прикладных программ, таких как MathCAD и Excel, которые обеспечили заданную точность в определении численных значений величин.
Приложение 1

Приложение 2
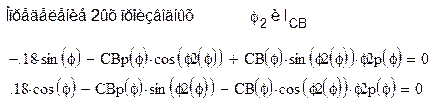
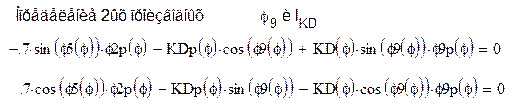
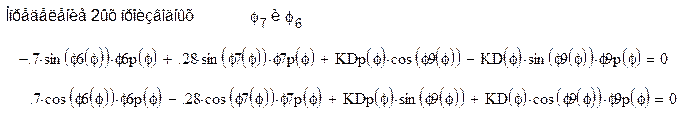
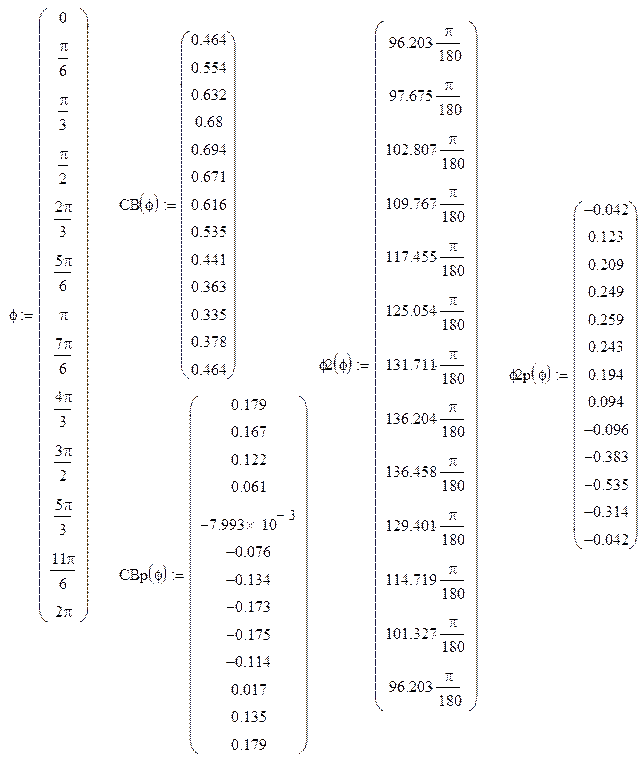
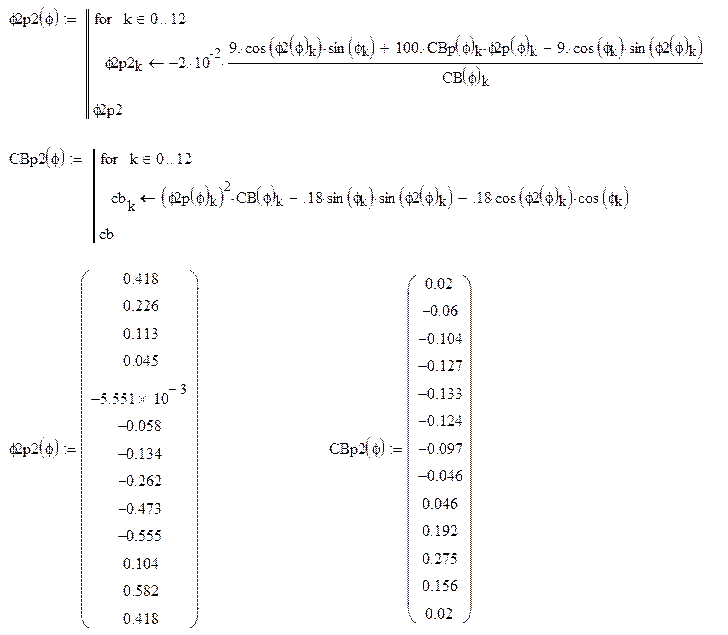
Аналогично определяем φ7p2(φ)
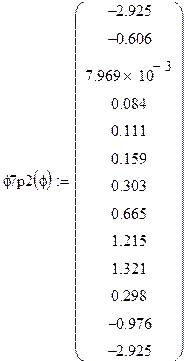
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.