Анализ и синтез механизма вязального аппарата, страница 3

, рад	’’	’’
0	0.418	-2.925
	0.226	-0.606
	0.113	0.0079
	0.045	0.084
	-0.005	0.111
	-0.058	0.159
	-0.134	0.303
	-0.262	0.665
	-0.473	1.215
	-0.555	1.321
	0.104	0.298
	0.582	-0.976
2	0.418	-2.925

2.6. Определение аналогов ускорений графическим методом.

2.6.1. Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем ω_= 1(1/с), ε₁=0(1/с²).

1. Определяем ускорение точки B₁, принадлежащей звену 1.

Чертим из полюса P_a отрезок произвольной длины, который параллелен AB - P_ab₁. Вводим

Масштабный коэффициент μ_a: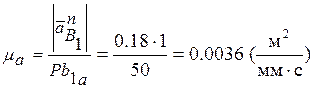

2. Строим ускорение точки B₂, принадлежащей звену 2.

             

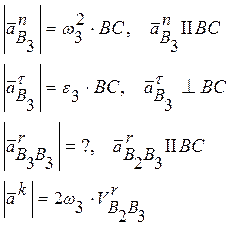
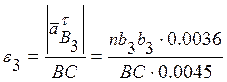
Для определения Кориолисова ускорения надо перпендикулярно вектору скорости на плане скоростей , провести прямую в сторону направления ω₃ , по этой прямой будет направлено Кориолисово ускорение. Строим из полюса прямую параллельную BC и откладываем на ней,

, направленный к точке C, получили точку nb₃.

Из точки b_1,b₂ чертим линию перпендикулярную BC, от b_1,b₂ откладываем Кориолисово ускорение.

В начало Кориолисово ускорения приходит вектор . Соединяем точку nb₃ с концом вектора  по прямой перпендикулярной BC. По этой прямой из конца вектора P_anb₃ выходит вектор  и заканчивается в точке b₃, которая является началом вектора . Определяем угловое ускорение звена по выше приведенной формуле.

3. Построение ускорений точек S₃ и  D аналогичны. Стоится прямая параллельная звену, на ней от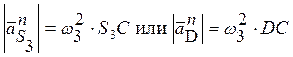кладывается . Из конца полученного вектора строится прямая перпендикулярная звену и на ней откладывается 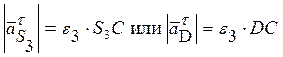. Вектор, соединяющий полюс и конец последнего вектора, является искомым вектором.

4. Определяем ускорение точки E. Рассматриваем ее движение относительно двух звеньев: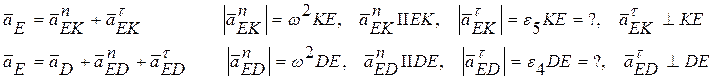

Из полюса чертим прямую параллельную прямой KE, на ней откладываем отрезок , направленный к точке K, получим точку nk. Из полученной точки чертим прямую перпендикулярную KE.

Из конца вектора ускорения точки D строим прямую параллельную DE, на ней откладываем вектор , получили точку nde. Из полученной точки строим прямую перпендикулярную DE. Точка пересечения прямой перпендикулярной KE, проведенной из точки nk, и прямой перпендикулярной DE, проведенной из точки nde, будет точкой e. Вектор, соединяющий полюс и точку e, будет равен модулю ускорения точки E.

И векторной диаграммы находим угловые ускорения звеньев 4, 5.

5. Определяем ускорение точки S₄:

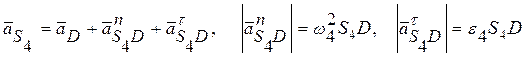
Чертим из конца вектора ускорения точки D прямую параллельную звену 4, на ней откладываем модуль нормальной компоненты вектора ускорения точки S₄, из полученной точки ns₄ проводим прямую перпендикулярнуюзвену 4, на ней откладываем модуль касательной компоненты вектора ускорения точки S₄. Вектор, соединяющий полюс и полученную точку s₄, является искомым вектором ускорения.

2.6.2. Результаты для положений 5 и 10 приведены в таблице 2.6.1

Таблица 2.6.1

	,м/с2	,м/с2	,м/с2	,м/с2	,м/с2	,м/с2
5π/6	0.18	0.1	0.054	0.11	0.15	0.13
5π/3	0.18	0.093	0.10	0.20	0.52	0.08

На рисунке 2.6.1 изображены зависимости угла φ₁ от углов , полученных аналитическим и графическим методами. На рисунке 2.6.2 Изображены зависимости угла φ₁ от положений звеньев механизма.

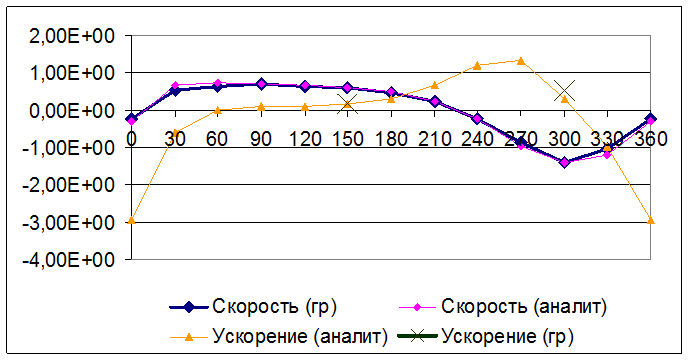
Рис. 2.6.1

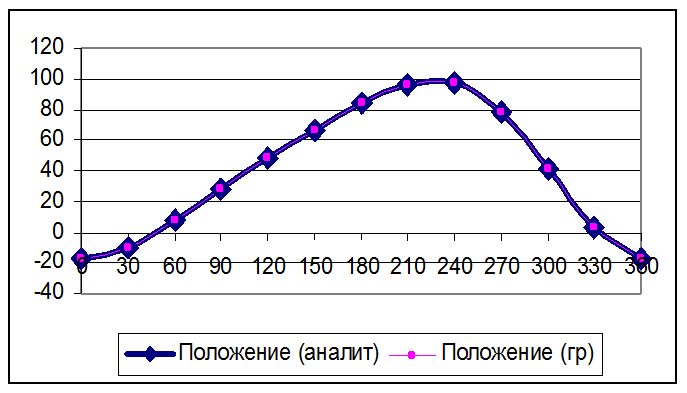
Рис. 2.6.2

Раздел 3. Силовой анализ.

Исходные данные

m3, кг	8,0
m4, кг	4,0
m5, кг	9,5
JS1,	0,04
JS3,	0,10
JS4,	0,20
JS5,	0,23
Fc, Н	400

Рассматриваем отдельно структурные группы Ассура. Начиная со звена 5.

1. Отмечаем все силы действующие на структурную группу - сила веса и момент инерции , приложенные к центру масс звена, неизвестные реакции, приложенные в точках соединения звеньев, направляя нормальную составляющую по звену, а тангенсальную перпендикулярно звену.

2. Составляем уравнение моментов, откуда находим тангенсальные составляющие реакций.

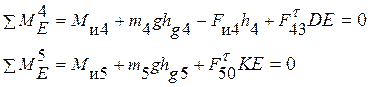
3. Составляем векторное уравнение равновесия всех сил, действующих на звено. Решая это уравнение графически, получаем оставшиеся нормальные компоненты реакций.

4. Мысленно разрывая кинематическую пару в структурной группе, определяем ее внутренние реакции. Составляя векторное уравнение всех сил, и решая его графически, получаем эти неизвестные.

5. Далее рассматриваем следующую структурную группу, применяя к ней все выше указанные действия, но при этом, зная силу, приложенную к точке присоединения этой структурной группы к предыдущей, которую уже исследовали. Эта сила будет равна по модулю  силе, которая является результатом сложения нормальной и тангенсальной компонент в этой точке, и противоположна ей по направлению.