Анализ и синтез механизма вязального аппарата, страница 2

, рад	0	0	0	0	, м
0	96,203	41,203	323,815	-17,105	0,464
	97,675	42,675	323,063	-10,641	0,554
	102,807	47,807	322,837	7,746	0,632
	109,767	54,767	325,841	28,157	0,68
	117,455	62,455	331,444	48,118	0,694
	125,054	70,054	338,2	66,786	0,671
	131,711	76,711	344,916	83,731	0,616
	136,204	81,204	349,857	96,114	0,535
	136,458	81,458	350,231	97,066	0,441
	129,401	74,401	342,469	77,626	0,363
	114,719	59,719	329,216	41,039	0,335
	101,327	46,327	322,613	2,748	0,378
2	96,203	41,203	323,815	-17,105	0,464

2.2. Графический метод определения положений звеньев механизма.

2.2.1. Определяем масштабный коэффициент μ_l.

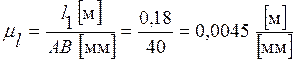
2.2.2. Определяем длины остальных звеньев механизма.

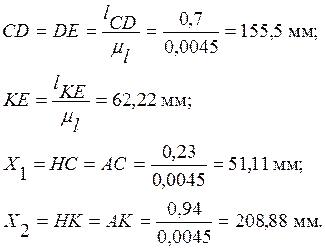
2.2.3. Результаты расчета положений звеньев при = представлены в табл. 2.2.

Таблица 2.2.

2.3. Определение аналогов скоростей аналитическим методом.

Продифференцировав уравнения (2.1), (2.2), (2.3) по обобщенной координате φ₁, выражаем скорости звеньев. Данный метод выполнен с помощью программы, написанной в MathCAD (приложение 1).

Таблица 2.3.1

, рад	’	’	’
0	-0.042	0.11	-0.316
	0.123	-0.221	0.682
	0.209	-0.189	0.738
	0.249	-0.125	0.702
	0.259	-0.065	0.664
	0.243	-0.014	0.606
	0.194	0.024	0.489
	0.094	0.025	0.243
	-0.096	-0.027	-0.249
	-0.383	-0.021	-0.961
	-0.535	0.179	-1.406
	-0.314	0.334	-1.212
2	-0.042	0.11	-0.316

2.4. Определение аналогов скоростей графическим методом.

2.4.1. Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем ω_= 1(рад/с).

1. Отмечаем полюс P_v, проводим через него прямую перпендикулярную звену AB, на ней отмечаем точку b₁ (b₂), так, что отрезок P_v b₁ (b₂)=40 мм. Определяем масштабный коэффициент

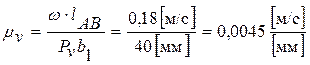
2. Проводим прямую параллельную BC через точку b₁ (b₂). Точка пересечения этой прямой с прямой перпендикулярной BC, проведенной через полюс, будет точка b₃ .

,             

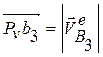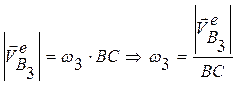
Отмечаем ω₃ на чертеже.

3. Проводим через полюс прямую перпендикулярную CD и на ней откладываем отрезок длиной , получаем точку d.

4. Проводим через полюс прямую перпендикулярную KE, по этой прямой направлена скорость точки E. Из точки d проводим прямую перпендикулярную P_vd. Точкой пересечения этих двух прямых будет точка e.

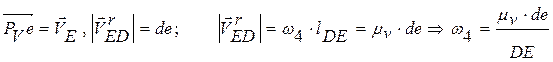
5. Проводим прямую перпендикулярную CS₃ через полюс и откладываем на ней отрезок длиной 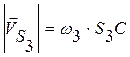. Это будет скорость точки S₃.

6. Проводим через полюс прямую перпендикулярную S₄D, откладываем на этой прямой отрезок длиной 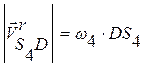. Складывая по правилу параллелограмма вектора 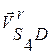 и , получаем скорость точки S₄.

Осуществляем все выше указанные действия для двенадцати положений механизма.

2.4.2. Результаты расчета скоростей точек звеньев при = представлены в табл. 2.4.1

Таблица 2.4.1

2.5. Определение аналогов ускорений аналитическим методом.

Продифференцировав дважды уравнения (2.1), (2.2), (2.3) по обобщенной координате φ₁, выражаем ускорения звеньев в двух положениях. Данный метод выполнен с помощью программы, написанной в MathCAD (приложение 2).

Таблица 2.5.1