Анализ и синтез механизма грохота

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ПРИКЛАДНОЙ МЕХАНИКИ

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к расчетно-графической работе по теории машин и механизмов

на тему: Анализ и синтез механизма грохота.

Автор проекта                                                  Маринин Н. Н.

Специальность                                                   средства поражения и боеприпасы

Обозначение проекта                                         РГР-2068956-40-12-04

Группа                                                                Ма21

Руководитель проекта                                     Капустин В.И.

Проект защищен                                                Оценка

Члены комиссии

НОВОСИБИРСК, 2004

задание на курсовой проект

BS3=1,2OB CS4=0,5CD

В качестве объекта исследования в курсовом проекте используется схема механизма грохота в соответствии с рис. 1.1.

Начальное положение – начало рабочего хода

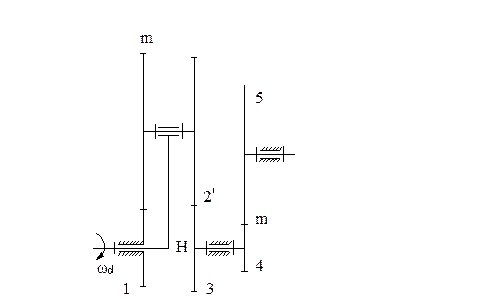
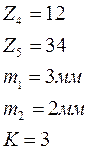
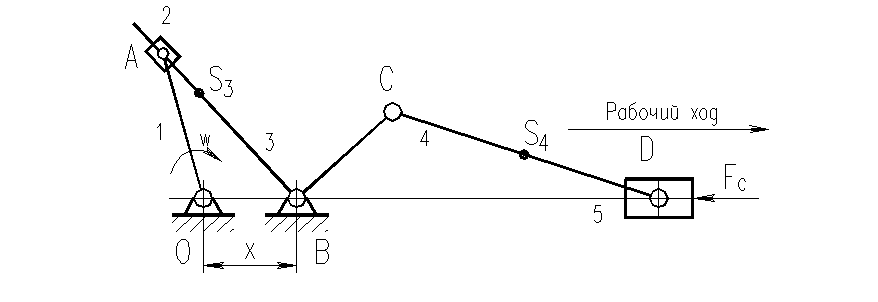
Рис. 1.1 Задание на анализ и синтез механизма грохота.

1. СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМА ГРОХОТА.

Структурный анализ механизма грохота проводим в соответствии с алгоритмом.

1.1.         Рисуем структурную схему механизма.

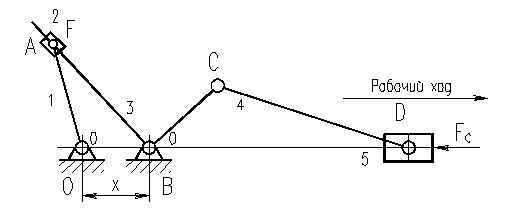
1.2.         Классифицируем кинематические пары механизма.

№ п/п	Номер звеньев, образую-щих пару	Условное обозначение	Название	Подвиж-ность	Высшая/ Низшая	Замыка-ние (Геометрическое/ Силовое)	Открытая/Закры-тая
1	0 – 1	O	Вращательная	I	Н	Г	З
2	1 - 2	A	Вращательная	I	Н	Г	З
3	2 - 3	F	Поступательная	I	Н	Г	З
4	3 - 0	B	Вращательная	I	Н	Г	З
5	3 – 4	С	Вращательная	I	Н	Г	З
6	4 – 5	D	Вращательная	I	Н	Г	З
7	5 – 0	E	Поступательная	I	Н	Г	З

Исследуемый механизм состоит только из одноподвижных кинематических пар (р₁ = 7, р = 7), р₁ – число одноподвижных кинематических пар в механизме, р – общее число кинематических пар в механизме.

1.3.         Классифицируем звенья механизма.

№ п/п	Номер звена	Условное обозначение	Название	Движение	Число вершин (t)
1	0	O B	Стойка (0)	Отсутствует	–
2	1		Кривошип (1)	Вращательное	2
3	2		Кулиса (3)	Вращательное	3
4	3		Камень (2)	Сложное	2
5	4		Шатун (4)	Сложное	2
6	5		Ползун (5)	Поступательное	2

Механизм имеет: четыре ( п₂ = 4 ) двухвершинных ( t = 2 ) линейных звена 1, 2, 4, 5; одно ( п₃ = 1 ) трехвершинное звено 3, которое является базовым ( Т = 3 ); пять ( п = 5 ) подвижных звеньев.

1.4.         Находим число присоединений подвижных звеньев к стойке. Исследуемый механизм грохота имеет три ( S = 3 ) присоединения к стойке.

1.5.         Выделяем в станке элементарные, простые и с разомкнутыми кинематическими цепями механизмы. В исследуемом сложном механизме можно выделить лишь один элементарный механизм

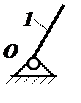
и два простых, один из которых является шарнирным трезвенником (кривошипно-ползунным),

 

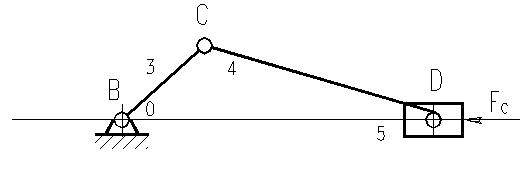
а второй – кулисным.

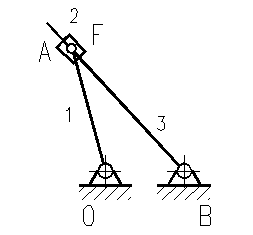
Механизмов с разомкнутыми кинематическими цепями в исследуемом механизме грохота нет.

1.6.         Выявляем простые стационарные и подвижные механизмы. Механизм грохота имеет в своем составе только простые стационарные механизмы.

1.7.         Находим звенья закрепления и присоединения. В исследуемом сложном механизме грохота звеньев закрепления нет. У него одно звено присоединения – звено 3 (кулиса). Звено 3 одновременно входит в два простых механизма – шарнирный трехзвенник и кулисный. Значит для этого звена К₃ = 2.

1.8.         Классифицируем механизм грохота. В соответствии с [1] исследуемый механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеют в своем составе только замкнутые кинематические цепи.

1.9.         Определяем подвижность простых механизмов. Анализ движений звеньев механизма и элементов кинематических пар [1] показывает, что исследуемые простые механизмы, да и сам сложный механизм существуют  в трехподвижном (П = 3) пространстве, в котором разрешены следующие простейшие независимые движения: два поступательных х и у вдоль соответствующих осей; одно вращательное j_Z вокруг оси Z.

Подвижность элементарных механизмов может быть определена по одной из следующих формул:

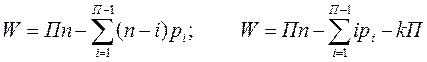
Формулы для определения подвижности этих механизмов примут вид соответственно:

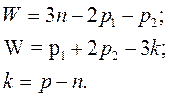
где W – подвижность механизма; п – число подвижных звеньев механизма; i – целочисленный индекс; p_i – число кинематических пар i-той подвижности;  – число независимых контуров; 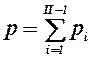 – общее число кинематических пар в механизме.

Определим подвижность шарнирного трехзвенника. Этот механизм имеет: три (n = 3) подвижных звена 3, 4, 5; четыре (р = р₁ = 4) одноподвижные кинематические пары В, C, D, E. Тогда его подвижность определиться:

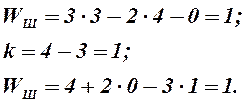
Найдем подвижность кулисного механизма. Кулисный механизм имеет: три (п = 3) подвижных звена 1, 2, 3 и четыре (р = р₁ = 4) кинематические пары О, А, F, В. Так как кулисный механизм по количественному и качественному составу кинематических пар и звеньев ничем не отличается от шарнирного трехзвенника, то его подвижность определяется по тем же формулам и также равна единице: