5. Записываем в проекциях на оси координат условия равновесия всех сил, действующих на звено 5:
![]() ,
откуда
,
откуда
![]() .
.
![]() ,откуда
,откуда
![]() .
.
Размеры длин звеньев берем из соответствующих планов положений.
![]()
Тогда
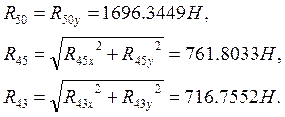
Помимо заданных сил и сил инерции, на
группу действуют реакции ![]() . Силы
представлены через их проекции на оси координат. Проекции R34x
и R34y найдены из анализа предыдущей группы:
. Силы
представлены через их проекции на оси координат. Проекции R34x
и R34y найдены из анализа предыдущей группы:

![]()
Для определения реакций в кинематических парах A и В (пользуясь диадой №2) записываем два уравнения проекций на оси и два уравнения моментов относительно точки В.
![]() для звеньев 2 и 3:
для звеньев 2 и 3:
![]()
Из уравнения выразим ![]() :
:
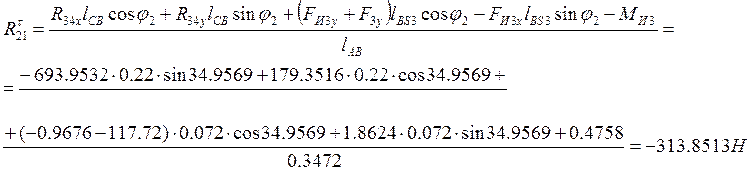
![]()
![]() для
звена 2:
для
звена 2:
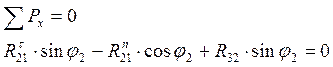 (4.2)
(4.2)
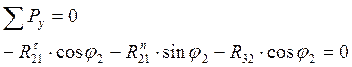 (4.3)
(4.3)
Из уравнения (4.2) выразим ![]() :
: 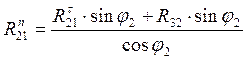 и
подставим в уравнение (4.3)
и
подставим в уравнение (4.3)
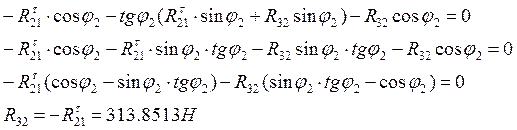
Полученное значение подставим в выражение (4.2):
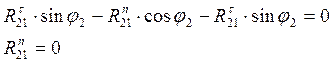
Тогда ![]()
![]() для
звена 3:
для
звена 3:
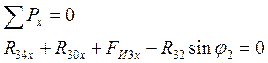 (4.4)
(4.4)
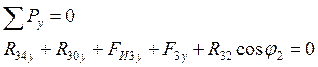 (4.5)
(4.5)
Из уравнения (4.4 ) получим:
![]()
Из уравнения (4.5 ) получим:
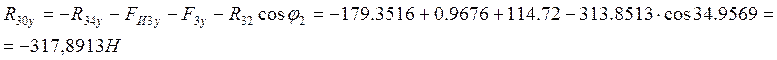
Тогда по теореме Пифагора найдем полную реакцию:
![]()
![]() для звена 3:
для звена 3:
![]()
Из уравнения выразим ![]() :
:
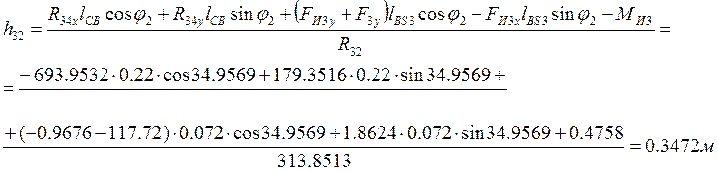
![]()
Отсюда видно, что реакция ![]() приложена в точке А (
приложена в точке А (![]() ).
).
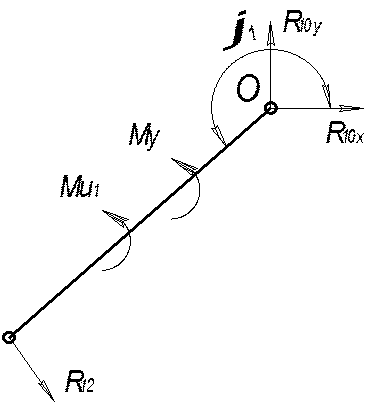
Для этого составляем уравнения равновесия начального звена механизма. Эти уравнения имеют следующий вид:
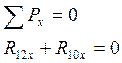
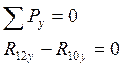
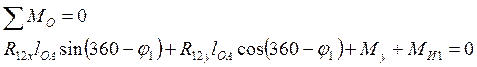
где ![]() ,
,
![]() ;
; ![]() ,
, ![]() – проекции на оси координат реакции
на звено 1 стойки 0;
– проекции на оси координат реакции
на звено 1 стойки 0; ![]() –
длина первого звена;
–
длина первого звена; ![]() – уравновешивающий момент.
– уравновешивающий момент.
Решая записанные выше уравнения, найдем
![]()
![]()
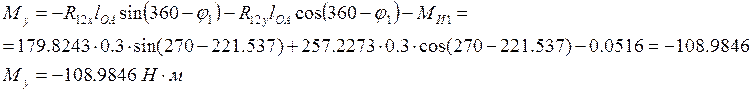
Полная реакция в опоре О будет определяться следующим образом:
Рисуем структурную группу 4-5, и прикладываем
к ней все силы и реакции. Под действием приложенных сил и моментов данная структурная
группа находится в равновесии. Определяем реакции R43 и R50 , которые представляем в виде тангенциальной
и нормальной составляющих ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Реакцию ![]() определим
из условия равновесия звена 4
определим
из условия равновесия звена 4
![]()
откуда
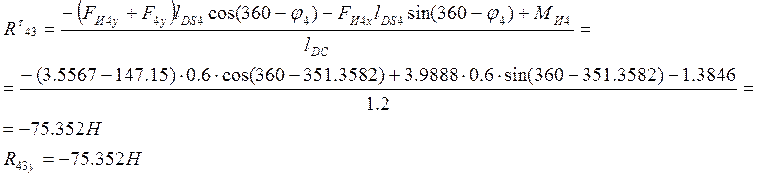
Реакции ![]() и
и![]() определим из условия равновесия группы
:
определим из условия равновесия группы
:
![]()
Принимаем масштаб плана сил µF= 1![]() и находим длины отрезков изображающие
на плане сил известные силы, входящие в уравнение:
и находим длины отрезков изображающие
на плане сил известные силы, входящие в уравнение:
(ab)=
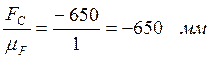 (bc)=
(bc)= 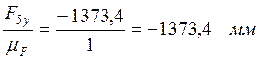
(cd)=
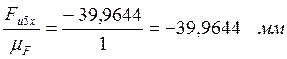 (de)=
(de)= 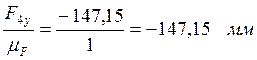
(fg)=
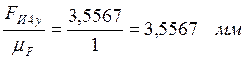 (ef)=
(ef)= 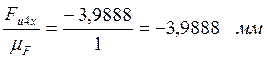
(gk)=
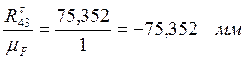
Выбираем свободное место на чертеже и последовательно в соответствии с векторным уравнением сил откладываем отрезки обозначающие силы.
Через точки а и h плана сил проводим линии действия нормальных
составляющих ![]() и
и ![]() соответственно.
соответственно.
![]() =(kh)mF=713,3749×1=713,3749 Н
=(kh)mF=713,3749×1=713,3749 Н
![]() =(ah)mF=1698,681×1=1698,681 Н
=(ah)mF=1698,681×1=1698,681 Н
Суммируя графически находим полные реакции
![]() ,
,
![]() =(gh)mF=717,3437×1=717,3437 Н
=(gh)mF=717,3437×1=717,3437 Н
Реакцию во внутренней кинематической паре D определяем графически, в соответствии с условием равновесия звена 5:
![]()
Суммируя графически находим
![]() (dh)mF=106,92×7=762,7968 Н
(dh)mF=106,92×7=762,7968 Н
Сравнительный анализ графического и аналитического исследования структурной группы 4-5 приведен в табл. 4.3.
Таблица 4.3
Сравнительный анализ графического и аналитического расчетов
|
Величина |
|
|
|
|
Графический метод |
717,3437 |
1698,681 |
762,7968 |
|
Аналитический метод |
716,7552 |
1696,3449 |
761,8033 |
|
Погрешность, % |
0.082 |
0.138 |
0.13 |
Изображаем отдельно группу 2-3 и прикладываем к ней все нагрузки и реакции в кинематических парах, со стороны звена 4 в паре C прикладываем реакции R34=- R43, определенную при анализе предыдущей группы 4-5.
Реакцию ![]() определим из условия равновесия звена 3
определим из условия равновесия звена 3
![]()
![]()
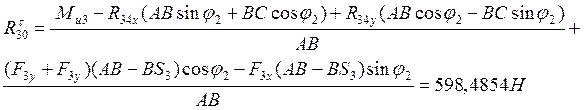
Реакцию ![]() определим из условия равновесия группы
определим из условия равновесия группы
![]() для звеньев 2 и 3:
для звеньев 2 и 3:
![]()
Из уравнения выразим ![]() :
:
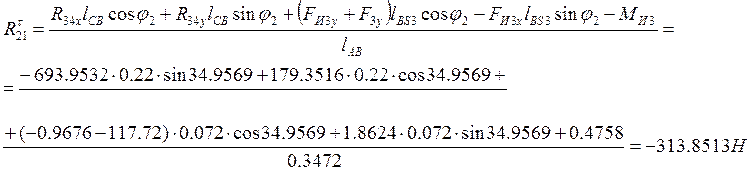
![]()
Реакции ![]() и
и ![]() определим
из условия равновесия группы:
определим
из условия равновесия группы:
![]()
Принимаем масштаб плана сил µF= 1 ![]() и находим длины отрезков изображающие
на плане сил известные силы, входящие в уравнение:
и находим длины отрезков изображающие
на плане сил известные силы, входящие в уравнение:
(ab)=
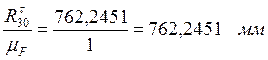 (bc)=
(bc)= 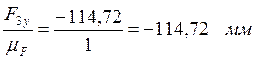
(cd)=
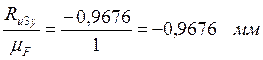 (de)=
(de)= 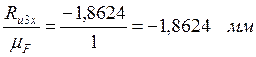
(fg)= 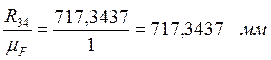
Выбираем свободное место на чертеже и последовательно в соответствии с векторным уравнением сил откладываем отрезки обозначающие силы.
Через точки а и f плана сил проводим линии действия ![]() и
и
![]() соответственно.
соответственно.
![]() =(ef)mF=313,8521×1=313,8521 Н
=(ef)mF=313,8521×1=313,8521 Н
![]() =(ga)mF=535,5214×1=535,5214 Н
=(ga)mF=535,5214×1=535,5214 Н
Суммируя графически находим полную реакцию
![]() ,
,
![]() =(gb)mF=931,5583×1=931,5583 Н
=(gb)mF=931,5583×1=931,5583 Н
Реакция во внутренней кинематической паре
A ![]() =
=![]()
![]()
Сравнительный анализ графического и аналитического исследования структурной группы 2-3 приведен в таблице 5.3.
Таблица 5.3
Сравнительный анализ графического и аналитического расчетов
|
Величина |
|
|
|
|
Графический метод |
931,5583 |
313,8521 |
-313,8521 |
|
Аналитический метод |
931,5579 |
313,8513 |
-313,8513 |
|
Погрешность, % |
4,3.10-5 |
0.0002 |
0.0002 |
Изображаем начальное звено,
прикладывая к нему реакции ![]() 12= -
12= - ![]() 21, найденную при анализе группы
2-3 , реакцию R10 и уравновешивающий момент Му
21, найденную при анализе группы
2-3 , реакцию R10 и уравновешивающий момент Му
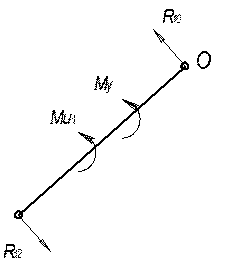
Му определяем из условия равновесия начального звена:
![]()
Реакцию R10 определим из уравнения:
R12+R10=0, откуда R10 =-R12,
R10=313,8513 Н
Находим погрешности определения реакции R10 и уравновешивающего момента Му соответственно:
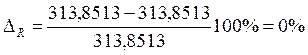
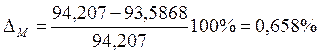
Синтез планетарной передачи состоит в подборе чисел зубьев колес и числа сателлитов по заданной схеме и передаточному отношению.
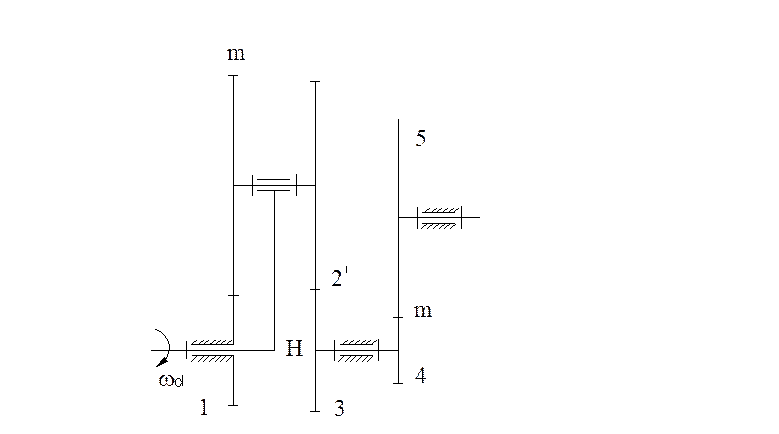
Схема механизма
При решении задачи используются условия соосности, сборки и соседства. Кроме того, числа зубьев колес должны находиться в приделах от 17 до 150.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.