Анализ и синтез механизма грохота, страница 2

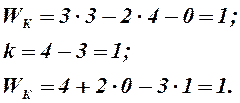
1.10.       Подвижность механизмов с незамкнутыми кинематическими цепями. Так как в механизме грохота нет механизмов с незамкнутыми кинематическими цепями, то нет необходимости определять их подвижность.

1.11.       Определяем подвижность сложного механизма. Подвижность сложного механизма исследуемого механизма грохота определяется по формуле.

.

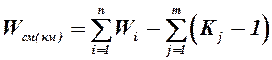Подставив в последнюю формулу значения из пп. 1.9 и 1.7, найдем

Так как исследуемый сложный механизм является однотипным, его подвижность  в соответствии с [1] также можно определять по формулам

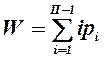
Подставив в эти формулы исходные данные (п = 5, р = р₁ = 7) из пп.1.3 и 1.4 , найдем подвижность этого сложного механизма:

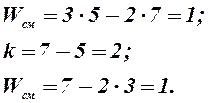
Видно, что полученные результаты совпадают.

1.12.       Выделяем структурные группы Ассура. В механизме грохота можно выделить следующие две структурные группы:

B                                                          

Видно, что выделенные структурные группы полностью подобны по видовому и количественному составу звеньев и кинематических пар. Каждая из структурных групп имеет: два подвижных звена (п’ = n’₂ = 2), три (р = 3) одноподвижные (р₁ = 3) кинематические пары, из которых две внешние (S’ = 2).

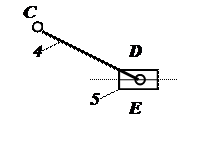
1.13.       Проводим классификацию структурных групп по И.И. Артоболевскому.

1.14.        Определяем класс сложного механизма. Механизм грохота относится ко II классу.2. Кинематический анализ механизма грохота.

2.1. Определение крайних (мертвых) положений механизма.

Так как механизм является кривошипно-ползунным, то крайними положениями будут такие положения, когда кривошип и ползун, то вытягиваются, то складываются в одну линию (рис. 2.1). Тогда определятся начальный и конечный углы φ_н = 281,537˚, φ_к = 78,463.

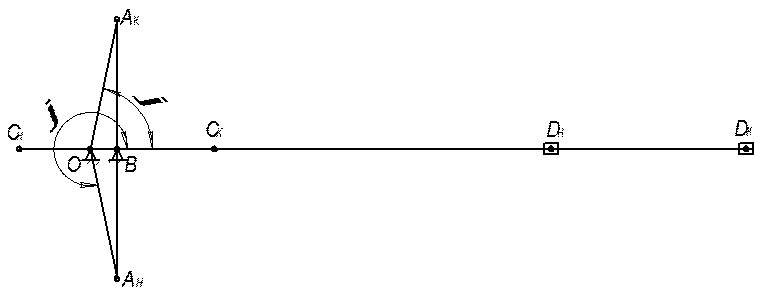
Рис.2.1. Крайние положения механизма грохота.

2.2. Определение положений звеньев механизма.

Для дальнейшего кинематического анализа, в частности, для определения положений звеньев и точек механизма, определения аналогов скоростей и ускорений графическим способом будем использовать угол, соответствующий шестому положению начального звена механизма            (φ₁ = 221,537˚). Аналитически будем проводить кинематический анализ для 36 положений механизма.

2.3. Построение планов положений исследуемого механизма.

Изображение кинематической схемы механизма, соответствующее определенному положению начального звена или начальных звеньев для механизмов с несколькими степенями свободы, называется планом механизма.

Построение планов положения (Рис 2.2.) проводим следующим образом

1. Выбираем место расположения стойки начального звена и, соблюдая принятые обозначения, вычерчиваем ее.

2. Радиусом 300 мм проводим тонкой линией траекторию движения начального звена (кривошипа).

3.  Определяем масштабный коэффициент длин

[м/мм],

где l_ОА – истинная длина кривошипа, ОА – выбранный чертежный размер кривошипа, ОА=300 мм.

=0,001 м/мм.

4.        В соответствии с формулой , находим чертежные и координатные размеры всех остальных размеров механизма, где АВ – чертежная длина звена, например, АВ; l_АВ – истинный размер звена.

–     отмечаем на чертеже неподвижные точки О и В, рисуем в них вращательные  кинематические пары;

–     проводим окружность радиусом ОА, которая является траекторией движения точки А;

–     на траектории движения точки А отмечаем шестое положение А₆ исследуемого механизма;

–     строим положения кривошипа, соединяя точку А₆ с точкой O;

–     методом засечек строим план положений механизма для каждого положения кривошипа;

       -результаты измерений заносим в таблицу 2.1;

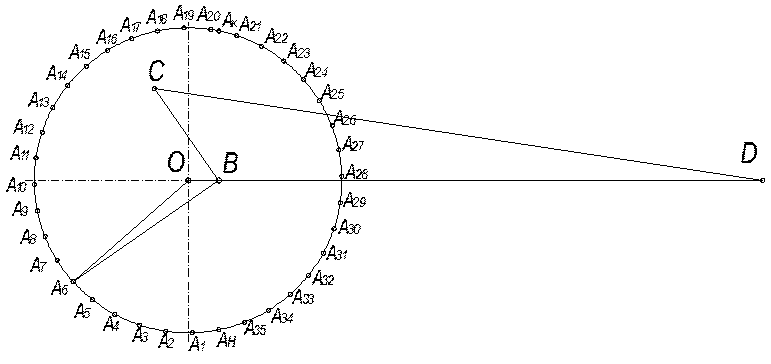
Рис 2.2 План расчетного положения механизма

Таблица 2.1

Чертежные размеры звеньев.

2.4. Кинематическое исследование машин и механизмов аналитическим методом.

Для определения кинематических характеристик механизма применим методом замкнутых векторных контуров.

Рис 2.3. Построение замкнутых векторных контуров.

1. Рисуем в любом промежуточном положении структурную схему исследуемого механизма.

2.        Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.

3.        В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.

4.        Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры: OA₆BO и ВСDB (Рис.2.3). Причем в каждый контур должно входить не более двух неизвестных величин.

Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора l₁, причем, все векторы совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие - со знаком «–»:

                                                (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат:

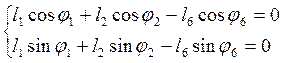                                       (2.2)

Среди величин, входящих в уравнение (2.2), переменными являются углы j₁  и j_2. Учитывая, что j₆ =0, преобразуем систему уравнений к следующему виду: