Анализ и синтез механизма грохота, страница 4

А₂- принадлежит камню;

А₃- принадлежит кулисе.

5)  Определим скорость точки А₃ :

, где  ,  и (2.28)

6)  Строим уравнение (2.28) на плане скоростей.

а) Проводим через полюс плана скоростей след скорости точки А₃ (^АВ);

б) Через точку а₂ проводим след скорости  (çêАВ) – след скорости поступательного движения камня по кулисе;

в) На пересечении следов получим точку а₃ . Согласно уравнению (2.28) расставим направление векторов.

7)  Находим истинное значение  м/с

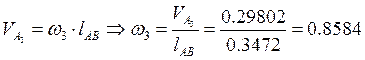 1/с

8)  Определяем направление w₃ , для чего мысленно переносим  в точку А₃.

9)  Определяем истинное значение

м/с

10)  Определяем скорость точки С:

 м/с

11)  Определяем скорость точки D : , где  ,   и

12)  Откладываем от полюса плана скоростей вектор V_C , длиной равной

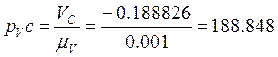 мм

13)  Проводим через полюс плана скоростей след скорости , так как эта скорость является абсолютной ().

14)  Проводим через полученную точку с  след скорости .

15)  Пересечение следов образует точку d.

16)  Найдем w₄:

Так как ,  то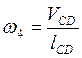

 м/с, тогда 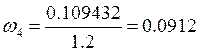 1/с

Найдем истинное значение  м/с

17)  Положение точек и на плане скоростей находим, воспользовавшись теоремой подобия:

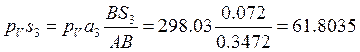мм

Находим истинное значение  м/с

Проекция на ось X:  

Проекция на ось Y:

18) 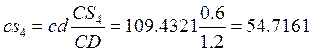  мм

Истинное значение  м/с

Проекция на ось X:

Проекция на ось Y:

Определяем аналоги линейных и угловых скоростей:

                                      

                            

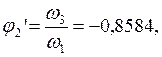
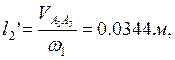
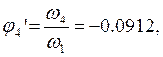
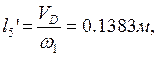
В табл. 2.6 приведены значения аналогов скоростей, полученные графическим и аналитическим методами.

Таблица 2.6.

Результаты расчета аналогов скоростей.

2.5.2. Определение аналогов ускорений исследуемого станка графическим методом.

Задачу решаем путем построения плана ускорений, считая w₁ постоянной величиной:

1)          Определяем ускорение точки А. Полное ускорение точки А равно нормальной составляющей, , которая направлена по линии ОА к центру O

, так как .

.

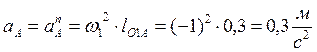2)          Из точки p полюса плана ускорений – откладываем вектор, изображающий ускорение точки А, в виде отрезка pа = 300 мм.

3)          Подсчитываем масштабный коэффициент плана ускорений:

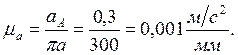
4)          Записываем векторное уравнение для определения ускорения точки А₃

                                   (2.29)

5)          Решим уравнение (2.29) относительно    . Следовательно,

                                   (2.30)

Распишем уравнение (2.30):                            (2.31)

где - нормальное ускорение точки А₃, ;

- тангенциальное ускорение точки А₃, ;

 – абсолютное ускорение точки А₂, ;

- кориолисово ускорение,;

- относительное ускорение, .

Кориолисово ускорение определяем по формуле

Нормальное ускорение точки А₃

6)          Уравнение (2.31) решаем графически. Через точку n₂ проводим линию, перпендикулярную АВ, и откладываем на ней отрезок n₂k, изображающий Кориолисово ускорение.

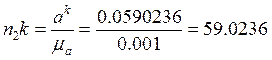 мм

Через точку k проводим линию, параллельную АВ, вдоль которой направлено относительное ускорение, а через полюс p - линию, параллельную АВ, и откладываем на ней отрезок pn₃, изображающий нормальное ускорение точки А₃.

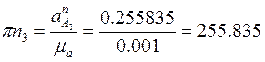 мм

Через точку n₃ проводим линию, перпендикулярную АВ, изображающую след ускорения . Пересечением следов ускорений и получим точку а₃, которую соединим с полюсом плана ускорений.

Найдем истинные значения

 м/с²

 м/с²

 м/с²

 

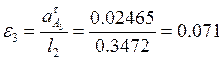
7)          Находим ускорение точки D

, где êêх; êêDС; .

Ускорения вычисляем по формуле:

 м/с²

 м/с²

 

 м/с²

Отрезки, изображающие в миллиметрах векторы этих ускорений, равны:

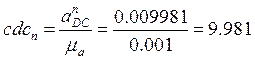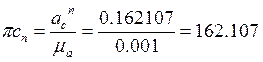 мм

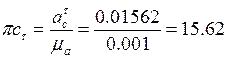 мм

 мм

Из полюса проводим линию, параллельную ВС, и откладываем отрезок pс_n.

 Из полюса проводим линию, перпендикулярную ВС, и откладываем отрезок pс_t. Сложением этих векторов получаем абсолютное ускорение точки С, истинное значение которого определим по формуле

 м/с²

Через точку с проводим линию, параллельную СD, и откладываем отрезок cdc_n , изображающий вектор .

Через точку dc_n проводим линию, перпендикулярную СD, изображающую след ускорения , пересечение которой со следом ускорения , параллельным оси Х и проходящим через полюс плана ускорений, образует точку d. Получим вектор, изображающий ускорение точки D, истинное значение которого равно:

 м/с²

Истинное значение  равно:

м/с²

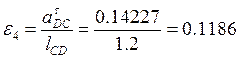
8)          Для нахождения ускорений точек S₃ и S₄ воспользуемся теоремой подобия.

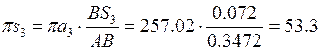мм

Проекция на ось Х: S_3x²= 46.41×10^-3

Проекция на ось Y: S_3y²= 26.21×10^-3

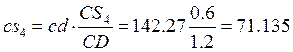 мм

Проекция на ось Х: S_4x²= 85.8×10^-3

Проекция на ось Y: S_4y²= -70.9×10^-3

Так как при построении плана ускорений звеньев мы приняли w₁ = const, то:

              

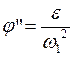
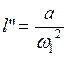
Учитывая, что 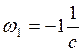, находим

                  

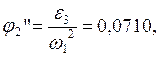
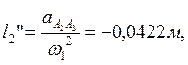
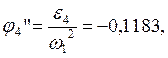
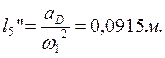
В табл. 2.7 приведены значения аналогов ускорений, полученные графическим и аналитическим методами.

Таблица 2.7.

Результаты расчета аналогов ускорений.