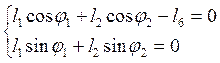Анализ и синтез механизма грохота, страница 3

.                                       (2.3)

Следовательно, из уравнений (2.3) находим угол наклона вектора `l₂:

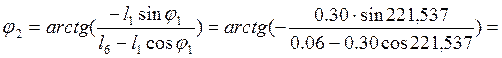34,9569°;              (2.4)

и его модуль:

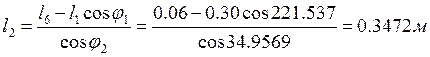                        (2.5)

Уравнение замкнутости второго контура ВСDB имеет вид:

                                                (2.6)

или в проекции на оси координат:

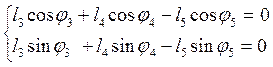.                                        (2.7)

Из геометрии видно, что угол j₃=j₂+90°=34,9569°+90°=124,9569°

Из системы уравнений (2.7) находим угол наклона вектора `l₄:

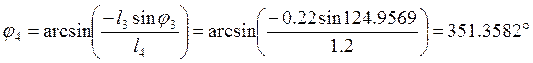
Для определения положений точек S₃ и S₄ записываем уравнения замкнутости контуров OAS₃О и ВCS₄В (Рис.2.2).

                                                 (2.8)

                                                (2.9)

Из уравнений (2.8) и (2.9) находим координаты центров масс третьего и четвертого звеньев:

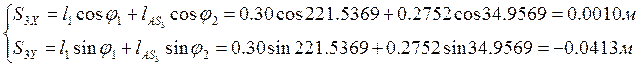       (2.10)

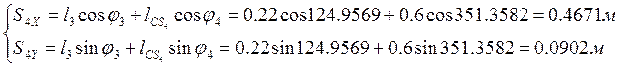  (2.11)

Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в табл. 2.2.

Таблица 2.2.

Результаты расчета положений звеньев.

Расчет для остальных тридцати шести положений представлен в таблице 2.3 в приложении 1.

Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = -1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.2) и (2.7). После дифференцирования уравнений (2.2) получим:

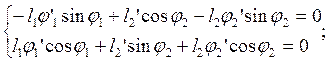                     (2.12)

где j₁’ – аналог угловой скорости звена 1. В расчетах принимаем       j₁’= -1 рад/с, так как угловая скорость звена 1 направлена по ходу часовой стрелки; j₂’ – аналог угловой скорости звена 2, l₂’ – аналог переносной (поступательной) скорости точки В.

Выразим из первого уравнения сиcтемы l₂ (2.12)

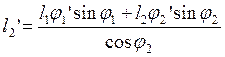;                                      (2.13)

Подставив полученное выражение во второе уравнение системы после ряда преобразований, получим:

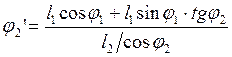;                                     (2.14)

Подставив в выражения (2.13) и (2.14) исходные данные в результате получим:

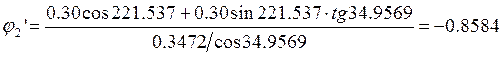
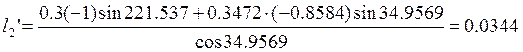
При дифференцировании уравнений (2.7) учитываем, что j₅’ = 0, получаем:

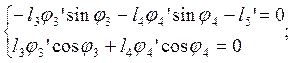        j₃’=j₂’                 (2.15)

Из первого уравнения системы (2.15) выразим l₅’

                                              (2.16)

Из второго уравнения системы (2.15) выразим j₄’

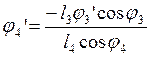                                         (2.17)

Подставив в выражения (2.13) и (2.14) исходные данные в результате получим:

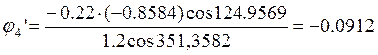
Аналоги скоростей центров масс звеньев 3 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.10) и (2.11):

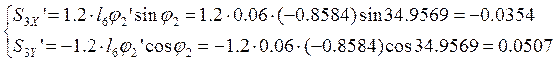   (2.18)

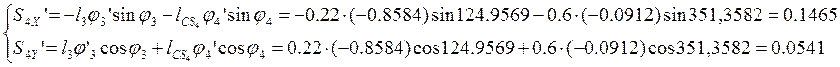(2.19)

Аналоги скоростей для тридцати шести положений механизма представлены в таблице 2.4.в приложении 2.

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.12) и (2.15). После дифференцирования уравнений (2.12) получим:

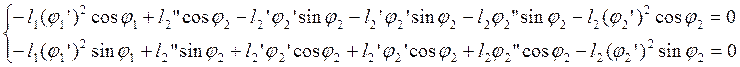
(2.20)

Выразим из первого уравнения системы (2.20) j₂”:

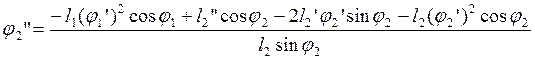                 (2.21)

Подставим (2.21) во второе уравнение системы (2.20) и выразим l₂”:

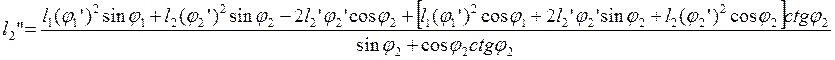                                                                                                                           (2.22)

Подставив в выражения (2.21) и (2.22) исходные данные в результате получим:

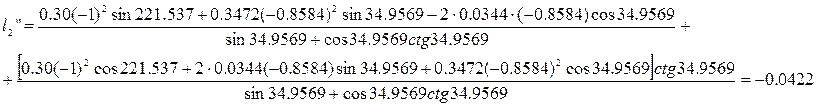
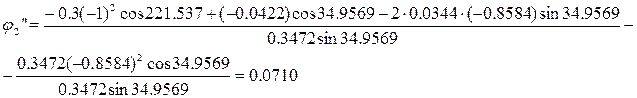
В результате дифференцирования системы уравнений (2.15) получим:

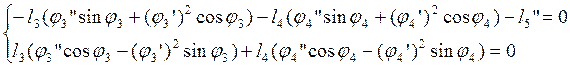           (2.23)

Из первого уравнения выразим l₅”:

                  (2.24)

Из второго уравнения выразим j₄”:

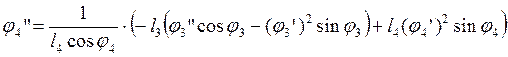           (2.25)

Подставив в выражения (2.24) и (2.25) данные в результате получим:

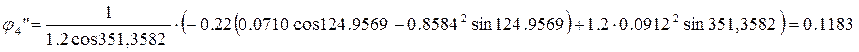
Дифференцируя по обобщенной координате уравнения (2.18) и (2.19), определяем аналоги ускорений центров масс звеньев 3 и 4 в проекциях на оси координат:

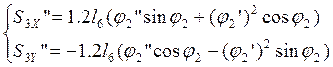                     (2.26)

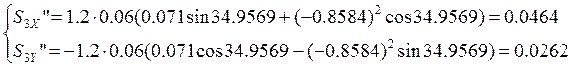
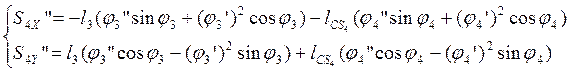(2.27)

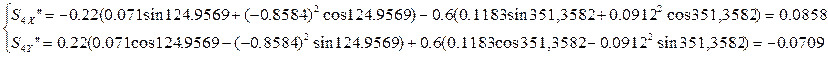
Результаты расчета аналогов ускорений для тридцати шести положений приведены в таблице 2.5.в приложении 2..

2.5. Построение планов скоростей и ускорений.

Планом скоростей (ускорений) называют рисунок, на котором в масштабе изображены векторы, равные по модулю и направлению скоростям (ускорениям) различных точек звеньев механизма в данный момент времени.

 План скоростей (ускорений) механизма, построенный для исследуемого положения механизма, является совокупностью нескольких планов скоростей (ускорений) отдельных точек звеньев, у которых полюса планов являются общей точкой – полюсом плана скоростей (ускорений) механизма.

2.5.1. Определение аналогов скоростей исследуемого станка графическим методом

Решение этой задачи графическим методом основано на построении плана скоростей для шестого положения механизма при j₁=221,537^о. Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

План скоростей строим в следующем порядке:

1)    находим линейную скорость точки А:

;

2)          из полюса плана скоростей р_V – откладываем перпендикулярно ОА отрезок р_Vа = 300 мм, изображающий вектор скорости точки А;

3)          находим масштабный коэффициент плана скоростей:

;

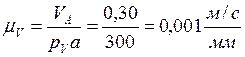4)  так как OAFB – представляет собой кулисный механизм, то  (^ОА), где точка А₁- принадлежит кривошипу;