Анализ и синтез механизмов сенного процесса

Министерство образования Российской Федерации

Новосибирский государственный технический университет

Кафедра прикладной механики

Пояснительная записка

К курсовому проекту по теории машин и механизмов

На тему: “Анализ и синтез механизмов сенного процесса”

Автор проекта                                                       Запорожец Н.С.

Специальность                                    1201, технология машиностроения  

          Обозначение проекта                          КП-2068956-40-15

          Группа                                                  КП-71

      Руководитель проекта                                          Смелягин А.И.

Проект защищен                         

Новосибирск, 1999

Новосибирский государственный                                          Технический Университет Пояснительная записка    Факультет         МТ                        Специальность    Группа               КП-71    Студентка          Запорожец Н.С.    Преподаватель  Смелягин А.И. 1999

1. Задание на проект

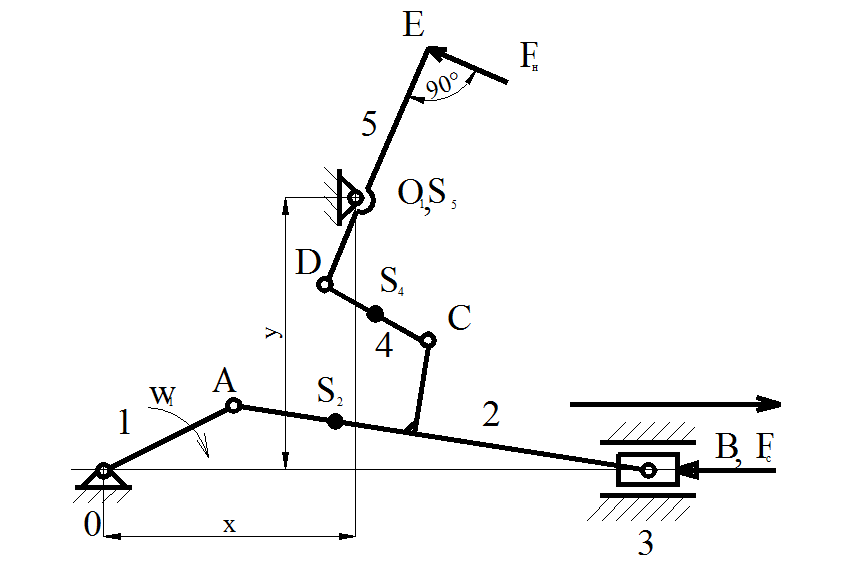
Выполнить структурный, кинетический и динамический анализ механизма сенного процесса.

Начальное положение – начало рабочего хода

 1.1.Структурный анализ механизма

  1.1.1.Структурная схема станка

 1.1.2.Выявляем сложные и разнесенные кинематические пары. Кинематическая пара E(F) является разнесенной и поэтому считаем ее как одну кинематическую пару Е.

1.1.3.Классифицируем кинематические пары механизма.

№	Номер звена образ. пару	Условное обозначение	Название	Подвиж-    ность	В/Н	Замыка-    ние	Открыт. Закрыт.
1	0-1		Вращател    ное	1	Н	Г	З
2	0-3		Вращател    ное	1	Н	Г	З
3	1-2		Вращател    ное	1	Н	Г	З
4	3-2		Поступа тельное	1	Н	Г	З
5	3-4		Вращател    ное	1	Н	Г	З
6	4-5		Вращател    ное	1	Н	Г	З
7	5-0		Поступа тельное	1	Н	Г	З

Иследуемый механизм состоит только из одноподвижных кинематических пар (p1 = 7, p = 7), где p1 – число одноподвижных кинематических пар в механизме, р – общее число кинематических пар в механизме.

1.1.4.Классифицируем звенья механизма.

№ п/п	Номер  звена	Условное обозначение	Название	Движение	Число вершин
1	0		Стойка(0)	Отсутствует	_
2	1		Кривошип(1)	Вращательное	2
3	2		Камень(2)	Сложное	2
4	3		Кулиса(3)	Вращательное	3
5	4		Шатун(4)	Сложное	2
6	5		Ползун(5)	Поступател.	2

Механизм имеет:

 пять подвижных звеньев (n=5)

 четыре (n2=4) двухвершинных (t=2) линейных звена 1,2,4,5,

 одно (n3=1) трехвершинное (t=3) звено 3.

1.1.5.Находим число присоединений к стойке.

 Механизм поперечно-строгального станка имеет три (S=3) присоединения к стойке.

1.1.6.Выделяем в станке простые, элементарные и с разомкнутыми цепями мханизмы.В исследуемом сложном механизме можно выделить один элементарный механизм

и два простых, один из которых является шарнирным

А второй кулисным

Механизмов с разомкнутыми кинематическими цепями в исследуемом попереуно-строгальном станке нет.

1.1.7.Выявляем простые стационарные и подвижные механизмы.

Станок имеет в своем составе только простые стационарные механизмы.

1.1.8.Выявляем звенья закрепления и присоединения.

В исследуемом сложном механизме звеньев закрепления нет. У него есть только одно звено присоединения – звено 3 (кулиса)

1.1.9.Классифицируем механизм станка. Исследуемый механизм имеет постоянную структуру, является сложным и однотипным. Он состоит из одного элементарного механизма и двух стационарных простых, которые имеют в своем составе только замкнутые кинематические цепи.

1.1.10.Определяем подвижность простых механизмов станка.

Анализ движений звеньев механизма и элементов кинематических пар показывает, что исследуемые простые механизмы, да и сам механизм существуют в трехподвижном (П=3) пространстве, в котором разрешены следующие простейшие независимые движения: два поступательных x,y вдоль соответствующих осей; одно вращательное jz  вокруг оси Z.

                               W=3n-2p1-p2

                                n=1, p1=1, p2=0      

                           W=3n-2p1-p2

                            n=2, p1=3

                            W=3n-2p1-p2   

                            n=2, p1=3

1.1.11. Подвижность механизмов с незамкнутыми кинематическими цепями. Так как в станке нет механизмов с незамкнутыми кинематическими цепями, то нет необходимости определять их подвижность.

1.1.13. Проводим анализ структурной модели механизма станка.

Проверяем, соответствует ли исследуемый механизм структурной математической модели. Механизм имеет: семь (р = 7) одноподвижных (р1 = 7) кинематических пар; пять (n = 5) подвижных звена, из которых одно (n3 = 1) базовое (Т=3) трехвершинное (t=3) и четыре (n2 = 4) двухвершинных (t=2); три присоединения к стойке (S = 3) и нет звеньев закрепления (Z=0).

Подставив эти исходные данные в математическую структурную модель, получим:

        7=0.5*(1*3+2*4+3)=7

        5=1+4=5                                           7=0.5*(1*3+2*4+3)=7

        k=7-5=2                                            5=1+4=5                                                                

       1=7-2*3=1                                         1=7-2*3=1

       7=7

Так как уравнения модели превратились в тождества, то исследуемое устройство имеет правильную структуру и является механизмом.

1.1.14.Выделяем структурные группы Ассура.

В механизме строгального станка можно выделить следующие две группы:

Проверяем, соответствуют ли выделенные структурные группы их математическим моделям.

Для первого звена          W=3n-2p1-p2=3*2-2*3=0

Для второго звена           W=3n-2p1-p2=3*2-2*3=0

Анализ полученных выражений показывает, что выделенные кинематические цепи являются структурными группами Ассура.

1.1.15.Проверяем, не распадаются ли выделенные структурные группы на более простые. Видно, что выделенные структурные группы являются самыми простыми для трехподвижного пространства, в котором существует механизм, и, значит, они не могут иметь в своем составе другие более простые группы Ассура.