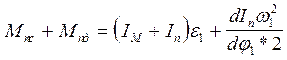 |
![]() Отсюда выразим :
Отсюда выразим :
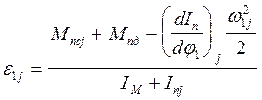 |
По данным формулам подсчитываем значения w1 и e1 в остальных положениях и полученные результаты заносим в таблицу.
4.Силовой анализ.
При силовом анализе механизма действующие силы должны быть известны, а подлежат определению уравновешивающий момент и реакции во всех кинематических парах. Решение этих задач основано на применении принципа Даламбера, согласно которому звено механизма можно рассматривать как находящееся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции.
Силовой анализ проводится для того, чтобы впоследствии по найденным силам произвести расчет на прочность элементов кинематических пар и звеньев механизма, а также правильно подобрать привод.
При силовом исследовании механизма обычно, по крайней мере, на первом этапе силами трения в кинематических парах пренебрегают, так как они часто невелики по сравнению с другими силами, действующими на механизм.
Силовой анализ механизмов проводят как аналитическими, так и графическими методами в соответствии со следующим алгоритмом:
1)определяют силы инерции звеньев;
2)выделяют структурные группы Ассура;
3)начиная с последней структурной группы, в которую входит выходное звено, последовательно определяют реакции во всех кинематических парах;
4)из условия равновесия начального звена находят уравновешивающий момент и реакцию, действующую на него со стороны стойки.
4.1.Определение сил, действующих на механизм.
4.1.1.Определение сил инерции.
Находим ускорения центров масс звеньев в проекциях на оси координат и угловые ускорения звеньев.
Для начального звена во втором положении соответственно будем иметь
![]() , e1=0
, e1=0
Для остальных звеньев ускорения центров масс и угловые ускорения находим по формулам, связывающими их с аналогами скоростей и ускорений, которые имеют вид:
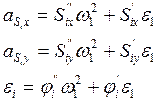 |
|||
(4.1)
В таблице ( ) приведены результаты расчета по формулам (4.1)
Для каждого звена механизма находим главный вектор и главный момент сил инерции:
Звено1: FИ1=0 , МИ1=0
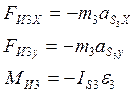 Звено3:
Звено3:
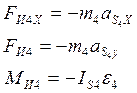 Звено4:
Звено4:
![]() Звено5:
Звено5:
![]()
4.1.2.Силы , действующие на механизм.
Для удобства дальнейшей работы в табл.( ) сведены все действующие на механизм силы и моменты в проекциях на оси координат со своими знаками.
Так как направления сил и моментов учтены их знаками, то на расчетных схемах все силы изображаем в направлении координатных осей, а моменты – против хода часовой стредки.
4.1.3.Рассматриваем равновесие структурной группы 4-5.
j4 = 178,78
ВС = 0,4м
СS4 = 0,2м
СS5 = 0,465
EC = 0,11м
CF = 1,04м
Yp = 0,1м
Запишем уравнение равновесия:

![]()
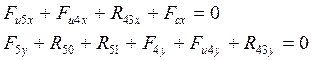
Запишем сумму моментов сил относительно точки С для каждого звена:
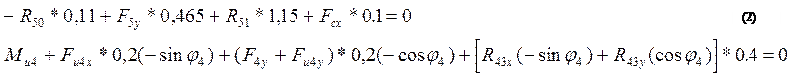 |
|||
Получаем систему:
![]()
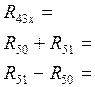
Решая сстему получим:
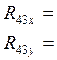 |
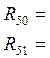 |
||
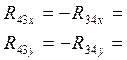 Значит :
Значит :
4.1.4.Рассматриваем равновесие структурной группы 3-2.
j3 = 96.95
O2A = 0.688м
O2S3 = 0.575м
O2B = 1,15м
AB = 0,462м
Запишем уранение равновесия:
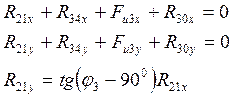 |
|||||
|
|||||
Запишем сумму моментов сил относительно точки О2 для каждого звена:
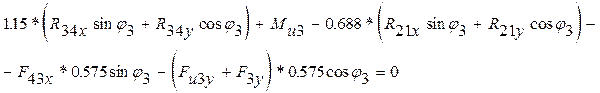 |
Получим систему уравнений:
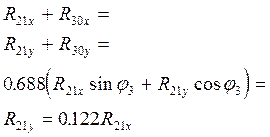 |
|||
Решая систему уравнений получим:
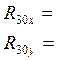
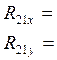
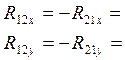 Значит:
Значит:
4.1.5.Рассматриваем равновесие начального звена.
j1=157,940
АО1 = 0,09м
Запишем уравнение равновесия:
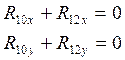 |
|||
Запишем сумму моментов сил отнасительно точки О1:
Получаем систему уравнеий:
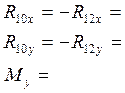 |
4.2.Определение уравновешивающего момента методом рычага Жуковского.
Теорема Жуковского применяется при решении многих задач динамики машин. В частности она используется для определения уравновешивающего момента (уравновешивающей силы), если нет необходимости в последовательном определении реакций в кинематических парах механизма.
В соответствии с теоремой Жуковского :
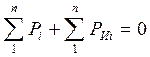 |
|||
|
|||
Уравнение (4.1.) равносильно уравнению моментов относительно полюса повернутого плана скоростей, т.е.
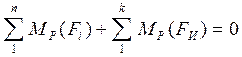 |
|||
|
|||
Из уравнения (4.2) находится уравновешивающий момент (уравновешивающая сила). Для этого строим повернутый на 90 градусов план скоростей механизма. К которому в соответствующих точках прикладываем заданные силы и силы инерции. Сохраняя их истинные направления.
Моменты инерции МИ1 , МИ3 , МИ4 заменяем парами сил FИ1FИ1 , FИ3FИ3 ,
FИ4FИ4соответственно, которые прикладываем перпендикулярно отрезкам О1А, О2B,BC.В точке С прикладываем уравновешивающую силу Fy b записываем уравнение моментов сил относительно полюса плана скоростей:
![]()
Отсюда
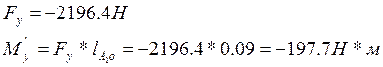 |
Сравним результаты полученные аналитическим и графическим методами:
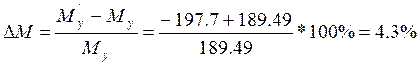 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.