Анализ и синтез механизмов сенного процесса, страница 4

Подставим численные значения во все полученные выражения:

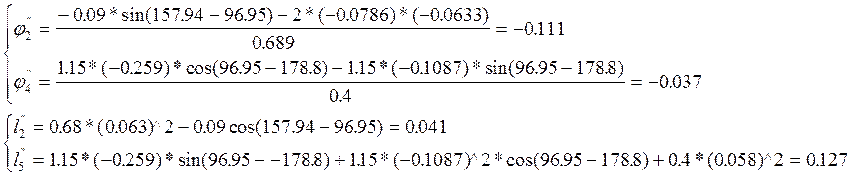
Найдем значения величин ускорения, т.к. в случае равномерного движения e1=0, то получим выражения :

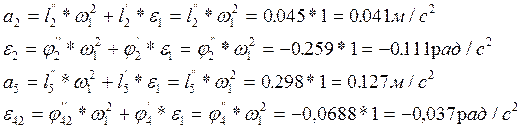Аналоги ускорений центров масс звеньев 3 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (7):

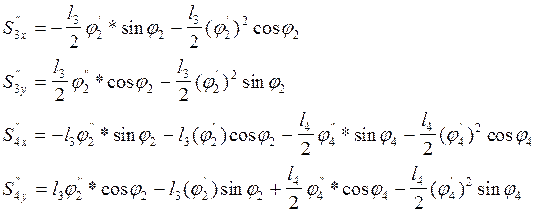Таблица сравнения аналитических и графических данных

Величина	j2	l2,м	j4	l5,м
Из плана ускорений	-0.1	0.041	-0.129	0.115
аналитическая	-0.099	-0.041	-0.029	0.114

3.Расчет маховика и динамическое исследование механизма.

Внутри цикла, установивщегося движения, угловая скорость начального звена машины периодически изменяется из-за постоянного изменения нагрузок, что приводит к нежелательной неравномерности движения. Неравномерность движения начального звена характеризуется коэффициентом неравномерности движения d, который не должен превышать допустимого значения [d]. Для снижения колебаний угловой скорости начального звена до допустимых пределов в машине предусматривают маховик, который с целью уменьшения его размеров устанавливают на быстроходном валу.

При определении момента инерции маховика IM вместо реального механизма рассматривают его одномассовую динамическую модель. Динамическая модель механизма состоит из одного, обычно начального звена, к которому приложены движущие силы Мnд, а также приведены все силы (моменты) Мnc, действующие на звенья машины и моменты инерции звеньев IM. Начальное звено также часто называют звеном приведения.

3.1.Определение параметров динамической модели.

2.1.1.Находим приведенный момент инерции:

где n – число звеньев, массы и моменты инерции которых даны;

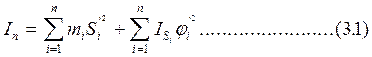mi – масса звена;

Isi – момент инерции звена относительно оси, проходящей через центр масс;

Si – аналог скорости центра масс звена;

ji – аналог угловой скорости звена.

Для рассматриваемого механизма формула (3.1) примет вид:

Где jд – аналог угловой скорости ротора двигателя.

Дифференцируя по обобщенной координате j1 выражение (3.2), находим производную приведенного момента инерции:

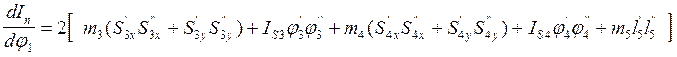Считаем значения In и dIn/dj1 для всех положений механизма. Полученные данные заносим в таблицу и по ним строим графики функции In=f(j1) и dIn/dj1= f(j1) (рис. 3.1). Начало координат графика размещаем в начале рабочего хода механизма.

3.3.Находим приведенный момент сил сопротивления

Приведенный момент сил сопротивления и веса определяем по формуле: 

Где n - общее число подвижных звеньев

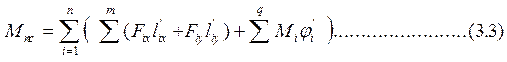      M – число сил, действующих на i-е звено

Fix, Fiy – проекции силы на соответствующие оси координат

lix, lix – проекции на соответствующие оси координат аналога скорости точки приложения силы

q – число моментов М, действующих на i-е звено.

Для исследуемого механизма формула (3.3) на рабочем и холостом ходе принимает вид соответственно:

В этих формулах f3y, f4y = проекции на ось Y сил веса звеньев 3 и 4, которые соответственно равны:

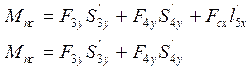F3y=-m3g=-20*9.8=-200 H

F4y=-m4g=-5*9.8=-50 H

Fcx=-Fc=-1.8 kH

Значения Mnc во всех положениях механизма приведены в таблице. В положениях, соответствующих началу действия силы резания и окончанию ее действия, подсчитаны два значения момента- с учетом силы резания и без нее.

3.4.Определение приращения кинетической энергии механизма.

 

Определяем работу момента Mnc , численным интегрированием функции Mnc=f(j1). Численное интегрирование проводим, используя метод трапеции, в соответствии с которым

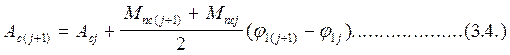Здесь j=1,2,…. номер положения механизма, для которого вычисляется работа. В начальном (нулевом) положении Ас0=0. Значения углов j1j подставляем в (3.4) в радианах.

Значения Ас, найденные по формуле (3.4), заносим в таблицу и по ним строим график функции Ас=f(j1).

В установившемся режиме работа Ас приведенного момента сил сопротивления за цикл равна работе приведенных движущих сил АПД. Считая, что привод развивает постоянный по величине приведенный момонт движущих сил МПД, найдем его величину:

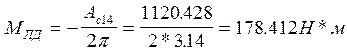Знак минус в последнем выражении указывает на то, что момент МПД направлен на преодоление приведенного момента сил сопротивления МПС. Строим график функции МПД=f(j1).

Работу АД приведенного момента движущих сил МПД вычисляем по формуле

Где i=1,2…- номер положения механизма.

Рассчитанные по формуле (3.5) значения работы движущих сил заносим в таблицу и по ним строим график функции АД=f(j1).

Находим закон изменения приращения кинетической энергии DT, для чего алгебраически складываем работы АД и АС

Где j =0,1,2…- номер положения механизма. Результаты вычислений заносим в таблицу и по ним строим график зависимости DT= f(j1).

3.5.Определение момента инерции маховика.

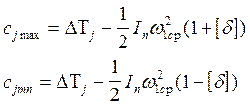Подсчитываем величины сjmax  и сjmin соответственно:

Где w1ср – средняя угловая скорость начального звена механизма.

 

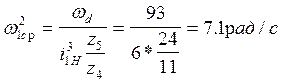Все вычисления заносим в таблицу.

Из величин            выбираем максимальную величину с_max=103.81Дж, а

 из         - минимальную с_min=-215.57Дж.

Необходимый момент инерции маховика в соответствии с формулой определится:

 

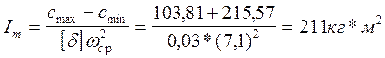3.5.Определение угловой скорости и углового ускорения начального звена мехапизма.

Угловую скорость звена приведения механизма находим по следующей формуле:

 

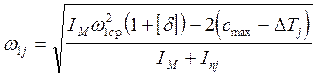Для определения углового ускорения e₁ запишем дифференциальное уравнение движения звена приведения: