4. Динамический анализ машины.
4.1. Определение параметров динамической модели.
Для построения динамической модели исследуемого станка в качестве звена приведения выбираем начальное звено (1), к которому приводим все силы (моменты), действующие на механизм и моменты инерции подвижных звеньев.
4.1.1. Приведённый момент инерции и его производная.
Приведённый момент инерции определяется по формуле, которая имеет следующий вид:
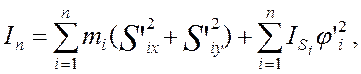 (4.1)
(4.1)
где n – число подвижных звеньев, массы и моменты инерции
которых заданы; ![]() - масса i-го звена;
- масса i-го звена;
![]() - момент инерции i-го
звена относительно оси, проходящей через центр масс;
- момент инерции i-го
звена относительно оси, проходящей через центр масс; ![]() -
проекции на оси координат аналога скорости центра масс i-го звена;
-
проекции на оси координат аналога скорости центра масс i-го звена; ![]() - аналог угловой скорости i-го
звена.
- аналог угловой скорости i-го
звена.
Для рассматриваемого механизма долбёжного станка формула (4.1) принимает вид:
![]() (4.2)
(4.2)
где 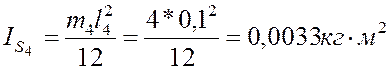
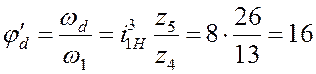 –
аналог угловой скорости ротора двигателя.
–
аналог угловой скорости ротора двигателя. 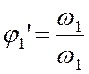 -
аналог угловой скорости начального звена.
-
аналог угловой скорости начального звена.
Дифференцируя по обобщенной координате ![]() выражение (4.2) находим производную
приведенного момента инерции:
выражение (4.2) находим производную
приведенного момента инерции:
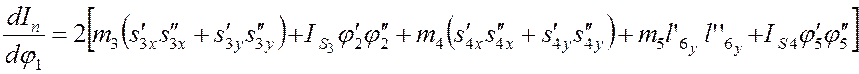 (4.3)
(4.3)
Считаем
значения ![]() и
и ![]() для
всех положений механизма. Полученные данные заносим в таблицу 4.1 и по ним
строим графики функции
для
всех положений механизма. Полученные данные заносим в таблицу 4.1 и по ним
строим графики функции ![]() и
и  (рис. 4.1). Начало координат графика
размещаем в начале рабочего хода механизма.
(рис. 4.1). Начало координат графика
размещаем в начале рабочего хода механизма.
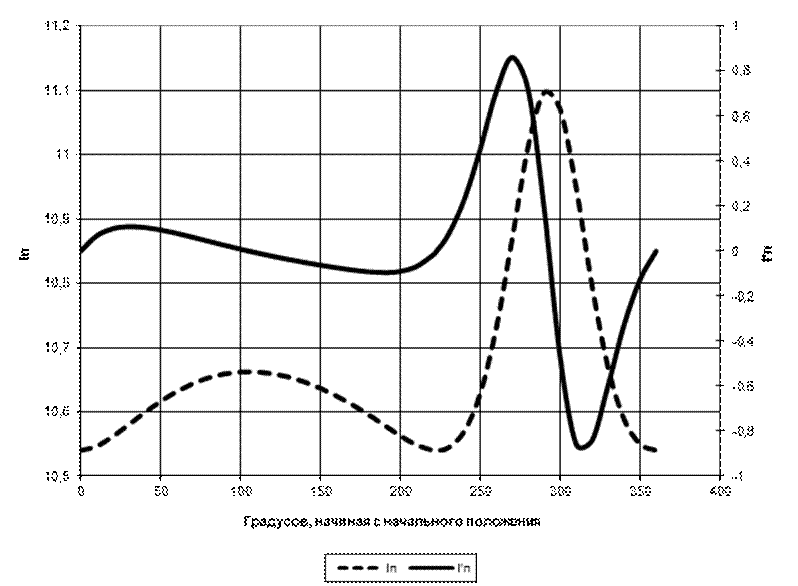
Рис.4.1. Диаграмма изменения приведенного момента инерции и его производной
4.1.2. Приведенный момент сил сопротивления
Приведенный момент сопротивления определяется по формуле, которая имеет следующий вид:
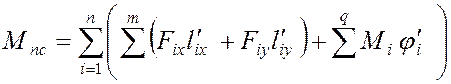 (4.4)
(4.4)
где n – общее число подвижных звеньев; m – число сил F, действующих на i-е
звено; ![]() – проекции силы на соответствующие оси координат;
– проекции силы на соответствующие оси координат; ![]()
![]() –
проекции на соответствующие оси координат аналога скорости точки приложения
силы; q – число моментов М, действующих на i-e звено.
–
проекции на соответствующие оси координат аналога скорости точки приложения
силы; q – число моментов М, действующих на i-e звено.
Для исследуемого станка формула (4.4) на рабочем и холостом ходе принимает вид соответственно:
![]() (4.5)
(4.5)
![]()
В формулах ![]() - проекции на ось Y сил веса звеньев (3), (4), (5), которые соответственно
равны:
- проекции на ось Y сил веса звеньев (3), (4), (5), которые соответственно
равны:
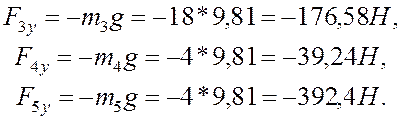 (4.6)
(4.6)
Сила
![]() действует при рабочем ходе ползуна
от точки
действует при рабочем ходе ползуна
от точки ![]() до точки
до точки ![]() .
Проекция силы сопротивления на ось Y определится
следующим образом:
.
Проекция силы сопротивления на ось Y определится
следующим образом: ![]() . Все остальные
составляющие, входящие в формулы (4.5), соответственно равны нулю.
. Все остальные
составляющие, входящие в формулы (4.5), соответственно равны нулю.
![]() (4.7)
(4.7)
![]()
Находим значение ![]() в
расчетном положении механизма
в
расчетном положении механизма
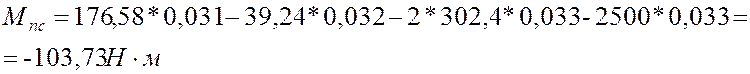
Значения Мпс в остальных положениях
механизма приведены в таблице 4.1. В
положениях, соответствующих началу действия силы долбления ![]() и окончанию ее действия
и окончанию ее действия ![]() , подсчитаны значения момента с
учетом силы
, подсчитаны значения момента с
учетом силы ![]() . Значения момента без учета силы
сопротивления даны ниже:
. Значения момента без учета силы
сопротивления даны ниже: ![]()
4.2. Определение приращения кинетической энергии механизма
Построив динамическую модель исследуемого механизма, приступим к ее
анализу. Анализ динамической модели будем проводить с помощью
графоаналитического метода Виттенбауэра. Для построения диаграммы необходимо
знать законы изменения приведенного момента инерции Iп и приращения кинетической энергии ![]() Т. Найдем закон изменения
приращения кинетической энергии.
Т. Найдем закон изменения
приращения кинетической энергии.
Сначала, в соответствии с (4.7) и
таблицей (4.1) строим график функции. При построении графика ![]() координатную систему
располагаем в начале рабочего хода исследуемого механизма (рис. 4.2). Затем
находим работу
координатную систему
располагаем в начале рабочего хода исследуемого механизма (рис. 4.2). Затем
находим работу ![]() приведенного момента сил сопротивления
приведенного момента сил сопротивления ![]() . Работу Ас определяем численным интегрированием функции
. Работу Ас определяем численным интегрированием функции ![]() . Интегрирование проводим, используя метод трапеций, в соответствии с
которым
. Интегрирование проводим, используя метод трапеций, в соответствии с
которым
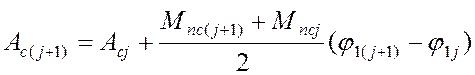 (4.8)
(4.8)
Здесь ![]() номер
положения механизма, для которого вычисляется работа. В начальном положении
номер
положения механизма, для которого вычисляется работа. В начальном положении ![]() .
.
Значения, найденные по формуле (4.8),
заносим в таблицу 4.1 и по ним строим график функции ![]() (рис.4.2).
(рис.4.2).
В установившемся режиме работа ![]() приведенного момента сил сопротивления за
цикл равна работе приведенных движущих сил
приведенного момента сил сопротивления за
цикл равна работе приведенных движущих сил ![]() . Считая, что привод развивает постоянный по
величине приведенный момент движущих сил
. Считая, что привод развивает постоянный по
величине приведенный момент движущих сил ![]() , найдем его величину
, найдем его величину
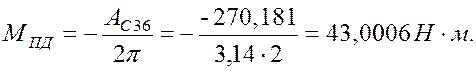
Знак минус указывает на то, что момент направлен на
преодоление приведенного момента сил сопротивления. Строим график функции ![]() (рис. 4.2).
(рис. 4.2).
Работу ![]() приведенного момента движущих сил вычисляем по формуле:
приведенного момента движущих сил вычисляем по формуле:
![]() , (4.9)
, (4.9)
где ![]() - номер положения механизма, для которого
определяется работа
- номер положения механизма, для которого
определяется работа ![]() . В начальном (нулевом) положении
. В начальном (нулевом) положении ![]() .
.
Рассчитанные по формуле (4.9)
значения работы движущих сил ![]() заносим
в таблицу (4.1) и по ним строим график функции
заносим
в таблицу (4.1) и по ним строим график функции ![]() (рис. 4.2).
(рис. 4.2).
Находим закон изменения приращения кинетической
энергии ![]() Т,
для чего алгебраически складываем работы
Т,
для чего алгебраически складываем работы ![]() и
и ![]() :
:
![]() (4.10)
(4.10)
где j = 0,1, 2… - номер положения механизма.
Результаты вычислений заносим в таблицу (4.1) и по ним строим график зависимости ![]() (рис.
4.2).
(рис.
4.2).
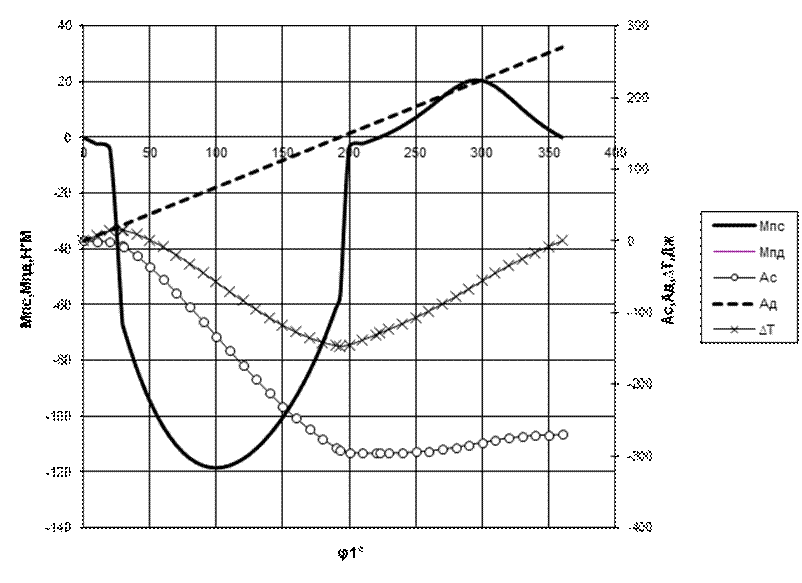 Рис. 4.2. Графики изменения
Рис. 4.2. Графики изменения ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
4.3. Определение момента инерции маховика.
Подсчитываем
величины ![]() и
и ![]() соответственно:
соответственно:
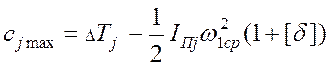 ,
, 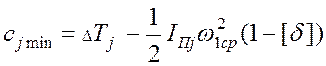 (4.11)
(4.11)
где 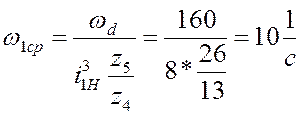 - средняя угловая скорость начального звена
механизма.
- средняя угловая скорость начального звена
механизма.
Найденные
значения ![]() и
и ![]() заносим
в таблицу (4.1). Из величин
заносим
в таблицу (4.1). Из величин ![]() выбираем наибольшую величину сmax = -534,653 Дж, а из
выбираем наибольшую величину сmax = -534,653 Дж, а из ![]() -
наименьшую cmin = -654,28 Дж.
-
наименьшую cmin = -654,28 Дж.
Момент инерции подсчитываем по формуле
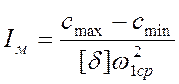 (4.11)
(4.11)
Подставляя исходные данные в формулу (4.11), получим
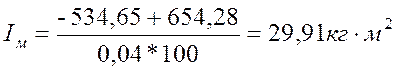 .
.
4.4. Определение закона движения начального звена и момента инерции маховика по диаграмме Виттенбауэра.
Диаграмму Виттенбауэра строим в системе координат ![]() Т = f(Iп) (рис. 4.3). Точки на диаграмме получаем,
откладывая значения координат Iпj и DТj, которые берем из таблицы (4.1) при одном и том же
значении обобщенной координаты
Т = f(Iп) (рис. 4.3). Точки на диаграмме получаем,
откладывая значения координат Iпj и DТj, которые берем из таблицы (4.1) при одном и том же
значении обобщенной координаты ![]() . Определяем
получившиеся в результате построения сетки масштабные коэффициенты осей
координат
. Определяем
получившиеся в результате построения сетки масштабные коэффициенты осей
координат ![]() и
и ![]() соответственно:
соответственно:
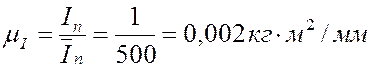 ,
, 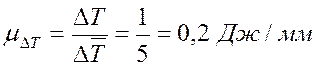 ,
,
где ![]() - отрезки, изображающие на диаграмме
истинные значения момента инерции и приращения кинетической энергии.
- отрезки, изображающие на диаграмме
истинные значения момента инерции и приращения кинетической энергии.
Вычисляем углы ![]() max и
max и ![]() min наклона касательных к диаграммам Виттенбауэра,
при реализации которых в механизме будет обеспечена требуемая неравномерность
движения:
min наклона касательных к диаграммам Виттенбауэра,
при реализации которых в механизме будет обеспечена требуемая неравномерность
движения:
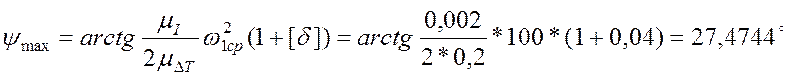 ,
, 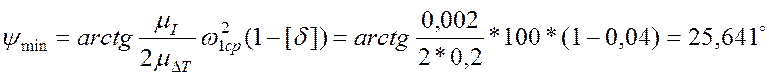 .
.
Проводим под углами ![]() max и
max и ![]() min к оси Iп касательные к диаграмме Виттенбауэра до пересечения с прямой,
параллельной оси
min к оси Iп касательные к диаграмме Виттенбауэра до пересечения с прямой,
параллельной оси![]() в точках q и p.
в точках q и p.
Необходимый момент инерции маховика подсчитываем по формуле:
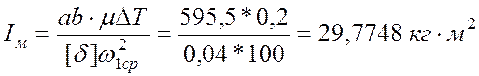 (4.12)
(4.12)
Отрезок ab находим из соотношения:
![]() (4.13)
(4.13)
Сравним величины момента инерции маховика, найденные аналитически и графически:
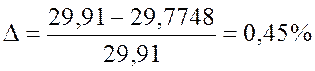

Рис. 4.3. Диаграмма Виттенбауэра.
4.5. Определение угловой скорости и углового ускорения начального звена механизма.
Угловую скорость звена приведения механизма находим по следующей формуле:
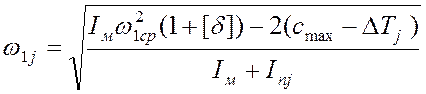 (4.14)
(4.14)
Для исследуемого механизма угловая скорость в расчетном положении определяется:
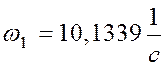 .
.
Для определения углового ускорения ![]() запишем
дифференциальное уравнение движения звена приведения
запишем
дифференциальное уравнение движения звена приведения
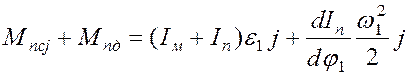 (4.15)
(4.15)
Из последнего уравнения находим ![]()
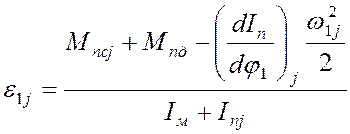 (4.16)
(4.16)
Тогда угловое ускорение ![]() исследуемого механизма в расчетном положении
определится:
исследуемого механизма в расчетном положении
определится:
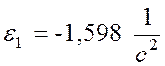 .
.
По формулам (4.11) и (4.13) подсчитываем значения ![]() и
и ![]() в остальных положениях. Полученные результаты заносим в таблицу (4.1).
в остальных положениях. Полученные результаты заносим в таблицу (4.1).
Таблица 4.1
Результаты динамического анализа механизма
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.