Кинематический анализ кулисного механизма с качающейся кулисой

2.КИНЕМАТИЧЕСКИЙ АНАЛИЗ МЕХАНИЗМОВ

2.1. Определение крайних (мертвых) положений механизмов.

Для кулисного механизма с качающейся кулисой крайними являются такие положения, когда кривошип и кулиса взаимно перпендикулярны.

 

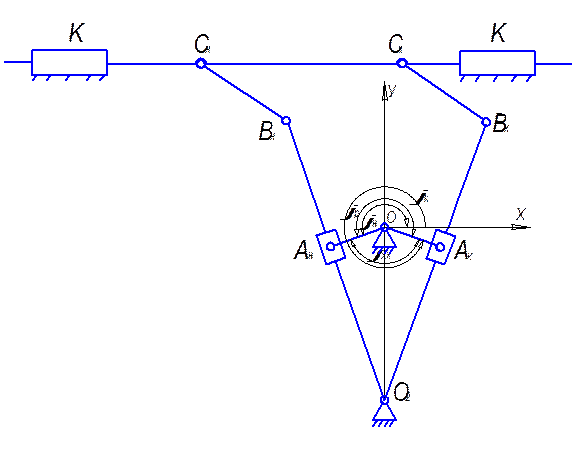
Рис.2.1. Определение крайних положений механизма вязального аппарата.

Рассмотрим прямоугольные подобные r ОА_нО₂ и r ОА_кО₂:

Получаем:

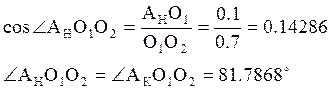
 - угол холостого хода механизма.

-  угол рабочего хода механизма;  - угол начального положения;

 - угол конечного положения.

2.2. Получение расчетного угла.

 Для дальнейшего кинематического анализа, в частности, для определения положений звеньев и точек механизма, определения аналогов скоростей и ускорений графическим способом будем использовать угол (f₁ = f_н  - 90° =98,213°). Аналитически будем проводить кинематический анализ для 36 положений механизма с применением программ Microsoft Excel и Mathcad.

2.3. Кинематическое исследование механизма аналитическим методом.

2.3.1. Построение замкнутых контуров методом Зиновьева. Определение положений звеньев механизма аналитическим методом.

Для определения линейных и угловых координат, скоростей и ускорений точек звеньев применим метод замкнутых  векторных контуров.

1. Рисуем  в любом промежуточном положении структурную схему исследуемого механизма.

2. Выбираем координатную систему. Начало координат помещаем в точку А – стойку начального звена.

3. Все звенья механизма  заменяем векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора (рис. 2.3).

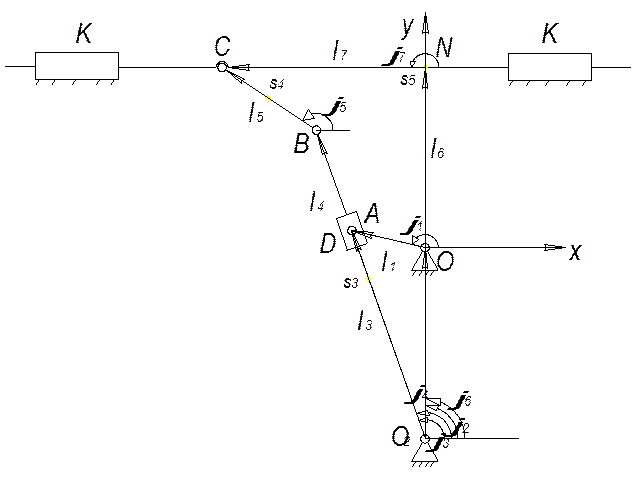
Рис. 2.2 Построение замкнутых векторных контуров

4. Полученные векторы объединяем между собой так, чтобы они образовали замкнутые контуры: О₂ОАО₂ и О₂NCBО₂. При образовании контура учитываем, что в него должно входить не более двух неизвестных величин.

Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора `l₁, причем, все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие – со знаком «-»:

                                                                                                                   (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат: 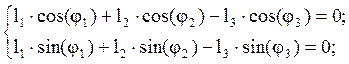                                                                                                                                   (2.2)

Среди величин, входящих в уравнения (2.2), переменными являются f₃, и l₃. Угол f₁является обобщенной координатой механизма и поэтому он должен быть задан. Из уравнений (2.2) подлежат определению  l₃, f₃.  Находим модуль вектора l₃ и угол наклона f₃:

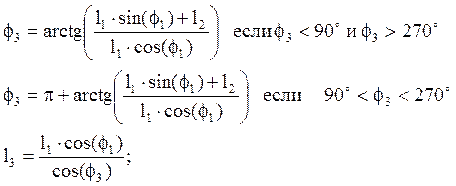                       (2.3)

Уравнение замкнутости контура О₂NCBО₂ имеет вид:

                                                             (2.4)

Уравнению (2.4) соответствуют два уравнения проекций на оси координат:                                                                                   

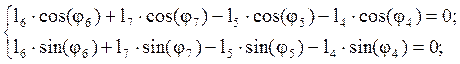                 (2.5)

Так как f₆=90^°, f₇=180^° то система уравнений  (2.5) примет вид:                                                             

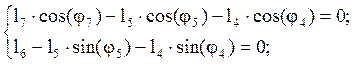                       (2.6)

Переменными являются в уравнения (2.6) f₅ и l₇. При этом f₃ = f₄.

Из (2.6) находим модуль вектора l₇ и угол наклона f₅:

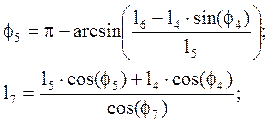                                          (2.7)

Для определения положений центров масс звеньев 3 и 4  S₃, S₄ записываем уравнения замкнутости контуров О₂ОS₃О₂ и О₂ВS₄О₂ (рис. 2.3).

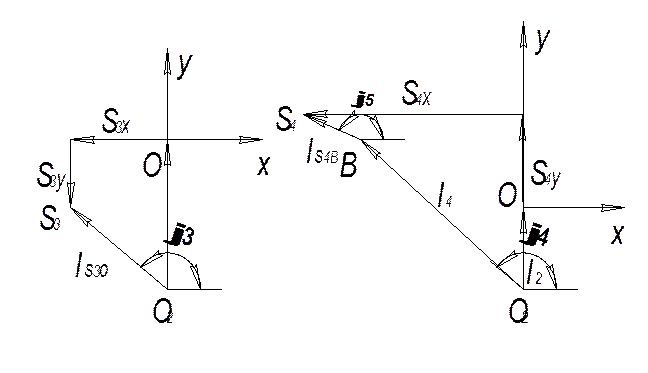
                   Рис.2.3. Построение замкнутых векторных контуров для S₃, S_4.

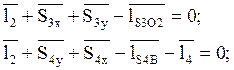                                         (2.8)

Из уравнений (2.12) находим координаты центров масс звеньев 3 и 4:

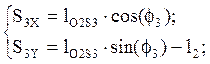                    (2.9)

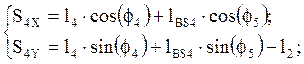      (2.10)

Положение центра масс 5 звена S₅ :

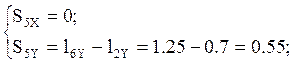
Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в (таб. 2.3.)

Расчет  положений для  тридцати шести значений представлен в (таб. 2.1.)

Таблица 2.1

Расчет положений для тридцати шести положений звеньев механизма