Кинематический анализ кулисного механизма с качающейся кулисой, страница 6

2.5.2. Определение аналогов ускорений исследуемого аппарата графическим методом

Задачу решаем путем построения плана ускорений, считая w₁ постоянной величиной:

1. Определяем  ускорение точки А. Полное ускорение точки А равно нормальной составляющей , которое направлено по линии АО к центру О: .

2. Из точки p - полюса плана ускорений - откладываем вектор, изображающий ускорение точки А₂, в виде отрезка pа₁ =50 мм (рис. 2.6).

3. Подсчитываем масштабный коэффициент ускорений:

;

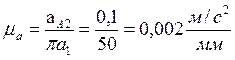4.  Ускорение точки А₃, которая является общей для звеньев 2 и 3 , находим из уравнения:

                                               (2.24)

Решаем уравнение (2.24) относительно а_А3:

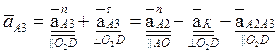,                              (2.25)

в котором  - относительное ускорение точки А₂ по отношению к точке А₃;

 - кориолисово ускорение, определяемое по формуле:

.

Направление кориолисова ускорения определяется поворотом относительной скорости  на 90° по  направлению переносной угловой скорости w₃ .

Уравнение     (2.25) решаем   графически (рис.  2.6). К вектору  пристраиваем вектор,  изображающий кориолисово ускорение:

.

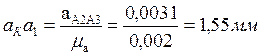Нормальное ускорение  вычисляем по формуле:

 .

Отрезок pn, изображающий  вектор этого ускорения, равен:

 .

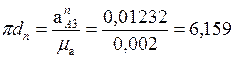
Вектор  направлен вдоль линии О₂D к центру . Через точку d_n плана ускорений проводим  линию в направлении касательного ускорения (ÖО₂D), а через точку a_K проводим линию, параллельную О₂D, вдоль которой направлено относительное ускорение. Точка пересечения  этих линий есть точка d – конец вектора ускорения точки A₃.

Вектора изображают ускорения  соответственно.

Найдем действительное значение ускорения точки А₃ и углового ускорения звена 3:

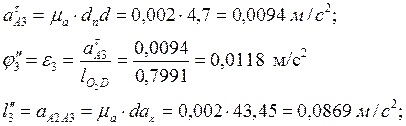
5. Для определения ускорения точки В записываем векторное уравнение:

                                                   (2.26)

Нормальную и касательную составляющие уравнения определяем по формулам  соответственно:

 

 .

Отрезки, изображающие векторы этих ускорений, равны:

,

.

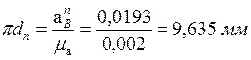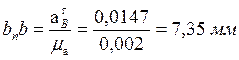Из плана скоростей найдем, что длина вектора pd, изображающего вектор , равна:

pd = 12,12 мм.

Найдем действительное значение ускорения точки B:

6. Для определения ускорения точки C запишем векторное уравнение:

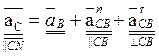                                          (2.27)

Нормальное ускорение  и отрезок ,его  изображающий вычисляем по формулам:

,

,

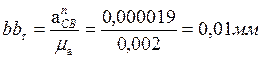К точке b пристраиваем вектор ,  который направлен вдоль линии CB к точке B; через точку  – линию, перпендикулярную BC;  через полюс p - вектор pc, параллельный CN, вдоль которой направлено  ускорение точки C.  Пересечение двух линий  есть точка c – конец вектора ускорения точки C.

Вектора  изображают ускорения соответственно.

pс = 7,53 мм, сb = 9,5 мм.

Найдем действительные значение ускорения точки С, и угловое ускорение звена 4:

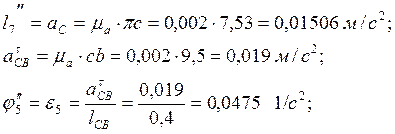
7. Ускорения центров масс S₃ и S₄ найдем по теореме подобия: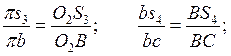

Откуда:

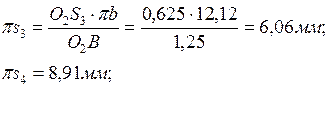
Истинное значение ускорения точек S₃, S₄:

8. Так как при построении плана ускорений мы приняли w₁ = const, то 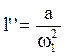 и  .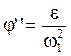

Учитывая, что , определяем аналоги линейных и угловых ускорений:

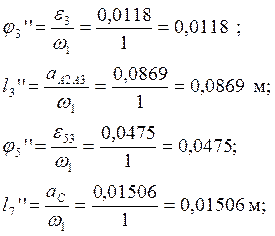
В таблице 2.7 приведены значения аналогов ускорений, полученные графическим и аналитическим  методами.

                                                                                   Таблица 2.7

Результаты расчета аналогов ускорений

Величина	l''3	f''3	l''7	f''5	S''3x	S''3у	S''4x	S''4y
Графически	0,0869	0,0118	0,01506	0,0475	-	-	-	-
Аналитически	0,0869	0,0117	0,01508	0,0475	0,0075	-0,0095	0,01507	-0,0095
Отклонение, %	0	0,84	0,13	0	-	-	-	-

                                                           Рис.2.6. План ускорений.