Кинематический анализ кулисного механизма с качающейся кулисой, страница 3

2.4. Нахождение положений исследуемого  механизма графическим методом

Изображение кинематической схемы механизма, соответствующее определенному положению начального звена или начальных звеньев для механизмов с несколькими степенями свободы, называется планом положений: выбираем место расположения стойки начального звена; радиусом 20 мм проводим тонкой линией траекторию движения начального звена (кривошипа); определяем масштабный коэффициент длин

m₁ = l₁ / ОА [м/мм],

где l₁ – истинная длина кривошипа, ОА – выбранный чертежный размер кривошипа, ОА= 20 мм

m₁ = 0,1/ 20 = 0,005 м/мм;

определяем отрезки, которые будут изображать на кинематической схеме остальные звенья механизма и координаты присоединений к стойке (табл. 2.2).

Таблица 2.2

Действительные и чертежные размеры звеньев

	ОA	О2В	ВС	ОО2	Х1	X2	ON
Действительные размеры l, м	0.1	1.25	0.4	0.7	0.6	0.46	0.55
Чертежные размеры, мм	20	250	80	140	120	92	110

Строим  планы положения механизмов при помощи программы Компас (рис 2.4).

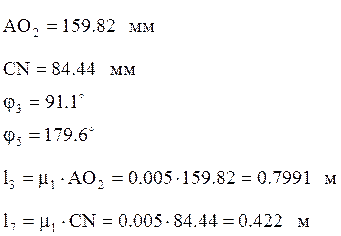
                                                                                                                               Таблица 2.3

                                          Результаты расчета положений звеньев

Номер положения	j1, град	j3, град	l3, м	j5,град	l7, м
Графически	98,213	91,1	0,7991	179,6	0,4222
Аналитически	98,213	91,02	0,7991	179,9	0,4223
Ошибка	0	-0,001	0	-0,002	0

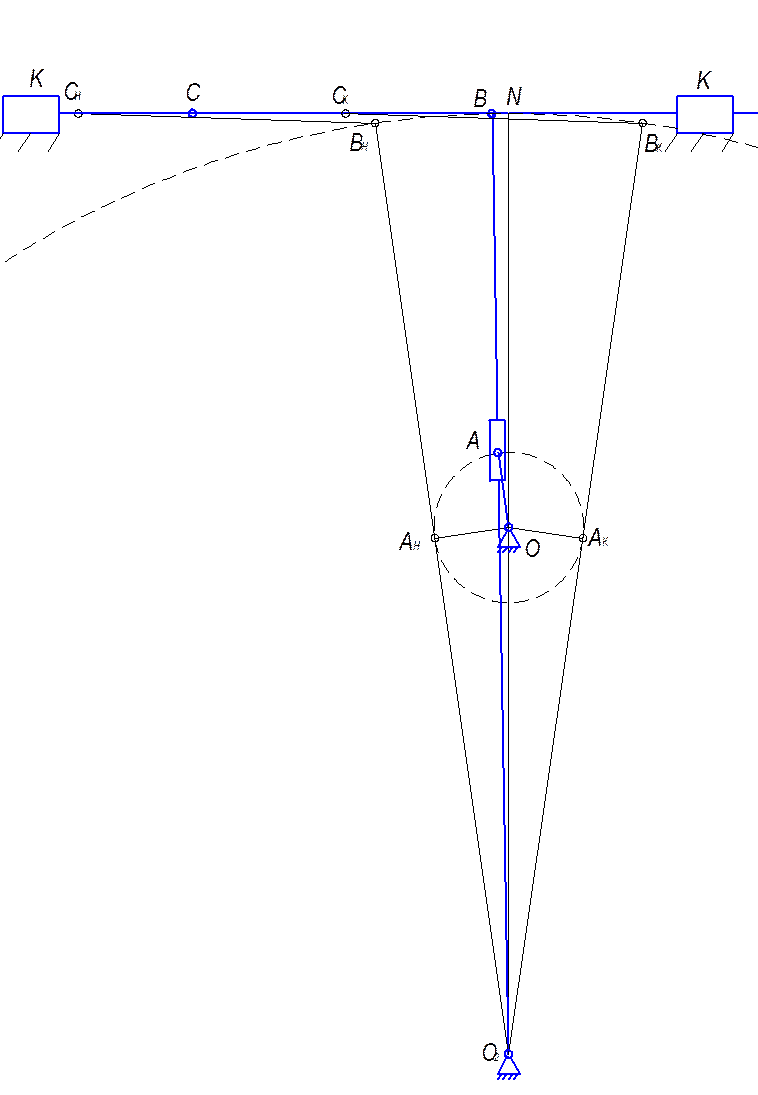                                              Рис.2.4 План положений механизма.

2.5. Определение аналогов скоростей  аналитическим методом

Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = -1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.2) и (2.6). После дифференцирования уравнений (2.2) получим:

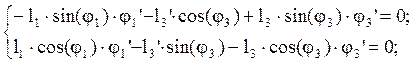          (2.11)

Найдем из (2.11) f₃’ и l₃’:

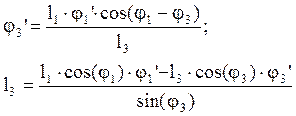                                                  (2.12)

После дифференцирования уравнений (2.6) получим:

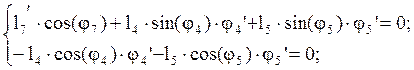        (2.13)

В этих уравнениях j₃’=j₄’ - аналог угловой скорости звена 3,  l₃’- аналог относительной скорости точки A, l₃’ - аналог  скорости точки C   и j₅’ - аналог угловой скорости звена 4:

Найдем из (2.17) l₇’и f₅’, учитывая, что f₃’=f₄’:

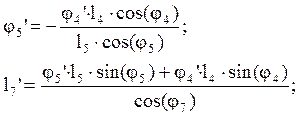                                                     (2.14)

Аналоги скоростей центров масс звеньев 3 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения  (2.13) и (2.14):

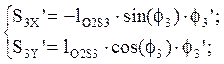                      (2.15)

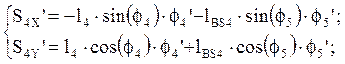 (2.16)

Аналог скорости центра масс звена 5 равен аналогу скорости точки С.

Расчет  аналогов скоростей для  тридцати шести значений представлен в (таб. 2.4.)

   Таблица 2.4

Аналоги скоростей для тридцати шести положений механизма