Кинематический анализ кулисного механизма с качающейся кулисой, страница 5

3. Подсчитываем масштабный коэффициент скоростей:.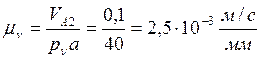

4. Скорость точки А, которая является общей для звеньев 2 и 3, находим, раскладывая движение точки  на переносное (поступательное) вместе с точкой А₃ и относительное (вращательное) вокруг  точки А₃:

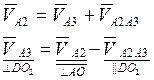,                                          (2.17)

Строим уравнение (2.26) на плане скоростей, для этого через точку a проводим линию, параллельную DO₂, а через полюс р_v –  линию,  перпендикулярную DO₂, до пересечения их в точке d.Векторы  изображают скорости V_А3   и V_A2А3 соответственно.

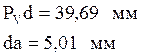
Найдем истинное значение скоростей :

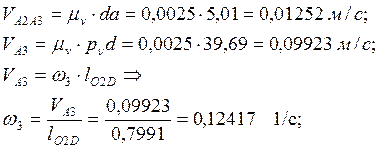
5. Находим скорость точки  СВ звена 4: м/с.

6. Находим скорость точки  С.  Для этого раскладываем плоскопараллельное движение звена 4 на переносное (поступательное) вместе с точкой В,  и относительное (вращательное) вокруг точки В.

Уравнение для скорости точки С:                        (2.18)

Строим (2.18) на плане скоростей. Из полюса р_v   проводим отрезок   перпендикулярный О₂В. Из  полюса р_v –  линию,  параллельную CN,а из точки b проводим прямую перпендикулярную ВС, до пересечения их в точке С. Вектора   изображает  соответственно скорости .

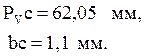
Найдем истинные значения скоростей:

 

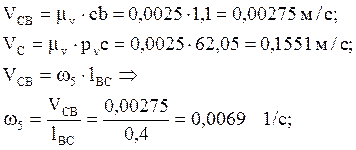
7. Скорости центров масс S₃ и S₄ найдем по теореме подобия: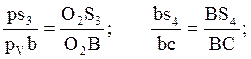

Откуда:

 

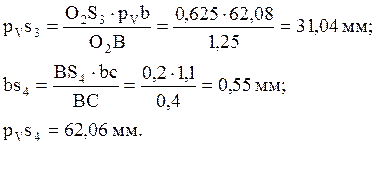
Истинное значение скорости точек S₃, S₄:

8. Определяем аналоги линейных и угловых скоростей:

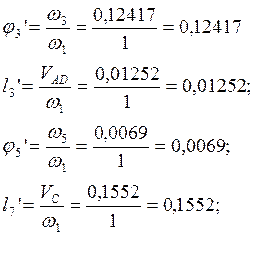
В таблице 2.5 приведены значения аналогов скоростей, полученные графическим и аналитическим методами.

                                                                                                                                Таблица 2.5

                                   Результаты расчета аналогов скоростей

Величина	f'3	l '3	f'5	l '7	S'3x	S'3у	S'4x	S'4y
Графически	0,12417	0,0125	0,0069	0,1552	-	-	-	-
Аналитически	0,12416	0,0125	0,0069	0,1552	0,0776	0,0014	0,1552	0,0014
Отклонение, %	0,02	0	0	0	-	-	-	-

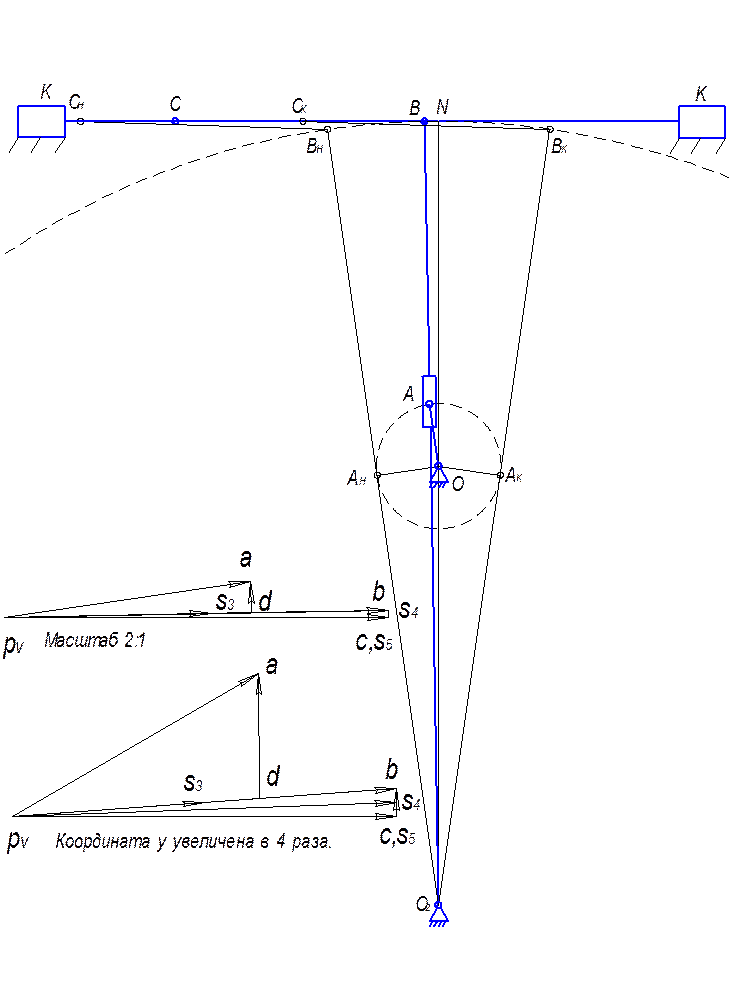
                                                             Рис.2.5. План скоростей.

2.7. Определение аналогов ускорений аналитическим методом

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений  (2.11) и (2.13).

После дифференцирования уравнений (2.11) получим:

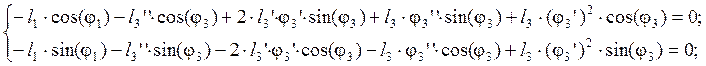(2.19)

В этих уравнениях j₃²=j₄² - аналог углового ускорения звена 3,  l₃²- аналог относительного ускорения точки А₃, Из  уравнений (2.19)  выражаем  соответственно  j₃² и l₃²:

 

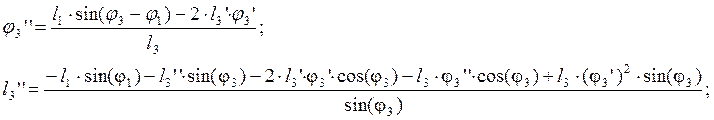
 После дифференцирования уравнений (2.13) получим:

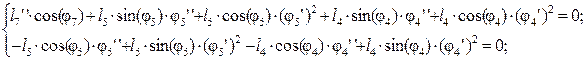 (2.20)  

 В этих уравнениях j₅² - аналог углового ускорения звена 5,  l₇²- аналог скорости точки С. Из  уравнений (2.20)  выражаем  соответственно  j₅² и l₇²:

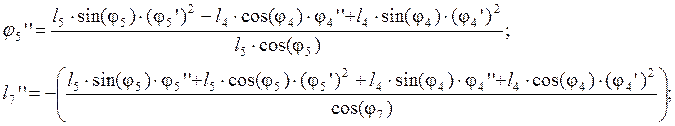(2.21)

Дифференцируя по обобщенной координате уравнения (2.15), (2.16), определяем аналоги ускорений центров масс звеньев 3 и 4 в проекциях на оси координат:

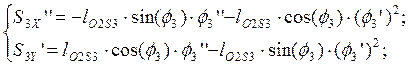 (2.22)

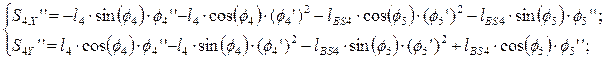      (2.23)

Аналог ускорения центра масс звена 5 равен аналогу ускорения точки С.

 

  Расчет  аналогов ускорений для  тридцати шести значений представлен в (таб. 2.6.)

   Таблица 2.6

Аналоги ускорений для тридцати шести положений механизма

f1,град	f3''	l3'', м	f5''	l7'', м	S3x'' ,м	S3y'', м	S4x'', м	S4y'', м
188,21	-0,144337	0	0,06447	-0,17774	0,08929	0,01289	0,17816	0,01289
178,21	-0,132019	-0,0167	0,05628	-0,16283	0,08174	0,01125	0,16316	0,01125
168,21	-0,117715	-0,0319	0,04299	-0,14582	0,07308	0,0086	0,14599	0,0086
158,21	-0,102408	-0,0453	0,02682	-0,12767	0,06384	0,00536	0,12767	0,00536
148,21	-0,086761	-0,0568	0,00969	-0,10895	0,05435	0,00194	0,10883	0,00194
138,21	-0,071175	-0,0665	-0,0068	-0,09003	0,04483	-0,00136	0,08984	-0,00136
128,21	-0,055857	-0,0744	-0,0216	-0,07109	0,03536	-0,00431	0,07091	-0,00431
118,21	-0,040877	-0,0804	-0,0336	-0,05226	0,026	-0,00672	0,05213	-0,00672
108,21	-0,02621	-0,0845	-0,0424	-0,03358	0,01673	-0,00848	0,03352	-0,00848
98,213	-0,011771	-0,0869	-0,0475	-0,01508	0,00753	-0,0095	0,01507	-0,0095
88,213	0,0025586	-0,0875	-0,0488	0,00327	-0,00164	-0,00975	-0,00327	-0,00975
78,213	0,0169125	-0,0863	-0,0461	0,02156	-0,01081	-0,00922	-0,02159	-0,00922
68,213	0,0314207	-0,0832	-0,0396	0,03989	-0,02003	-0,00793	-0,03997	-0,00793
58,213	0,0461924	-0,0784	-0,0296	0,05836	-0,02933	-0,00593	-0,05851	-0,00593
48,213	0,0612941	-0,0718	-0,0166	0,07709	-0,03874	-0,00331	-0,07728	-0,00331
38,213	0,0767216	-0,0633	-0,0011	0,09611	-0,04823	-0,00021	-0,09628	-0,00021
28,213	0,0923624	-0,0529	0,01581	0,11533	-0,05775	0,00316	-0,11542	0,00316
18,213	0,1079463	-0,0407	0,0328	0,13448	-0,06718	0,00656	-0,13442	0,00656
8,213	0,1229862	-0,0267	0,04818	0,15299	-0,07627	0,00963	-0,15276	0,00963
358,21	0,1367116	-0,0109	0,05991	0,16994	-0,0846	0,01198	-0,16957	0,01198
348,21	0,1480136	0,00632	0,06572	0,18397	-0,09157	0,01314	-0,18356	0,01314
338,21	0,1554262	0,02473	0,06346	0,1933	-0,09631	0,01269	-0,19296	0,01269
328,21	0,1571915	0,04376	0,05164	0,19575	-0,09773	0,01033	-0,19561	0,01033
318,21	0,1514583	0,06264	0,03013	0,18904	-0,09461	0,00603	-0,18912	0,00603
308,21	0,1366505	0,08037	0,00088	0,17112	-0,08581	0,00018	-0,17137	0,00018
298,21	0,1119788	0,09577	-0,0317	0,14082	-0,07069	-0,00634	-0,14109	-0,00634
288,21	0,0779641	0,1076	-0,0614	0,0985	-0,04943	-0,01227	-0,09868	-0,01227
278,21	0,0367424	0,11478	-0,0813	0,04663	-0,02336	-0,01626	-0,04667	-0,01626
268,21	-0,008082	0,11658	-0,0865	-0,01029	0,00514	-0,01731	0,01028	-0,01731
258,21	-0,052102	0,11281	-0,0757	-0,06636	0,0331	-0,01514	0,06628	-0,01514
248,21	-0,091095	0,10386	-0,0516	-0,11578	0,05767	-0,01031	0,11556	-0,01031
238,21	-0,121929	0,09062	-0,0201	-0,15423	0,07683	-0,00401	0,15394	-0,00401
228,21	-0,143058	0,07424	0,012	-0,17974	0,08966	0,0024	0,17953	0,0024
218,21	-0,154479	0,05597	0,03886	-0,19266	0,09632	0,00777	0,19265	0,00777
208,21	-0,157327	0,03693	0,05701	-0,19492	0,09768	0,0114	0,19514	0,0114
198,21	-0,153329	0,01804	0,06531	-0,18912	0,09494	0,01306	0,1895	0,01306