3. Кинематический анализ механизма комбайна.
3.1 Определение крайних (мертвых) положений механизма.
Для данного механизма крайними будут такие положения, когда кулиса и шатун то вытягиваются, то складываются в одну линию (рис 3.1).
.

Рис 3.1. Крайние положения механизма.
Находим значения углов ![]() ,
, ![]() ,
, ![]() ,
, ![]() (табл.3.1)
(табл.3.1)
Т а б л и ц а 3.1.
Крайние положения механизма.
|
Углы |
φн° |
φк° |
φрх° |
φхх° |
|
Значения |
351 |
189 |
198 |
162 |
3.2. Определение положений звеньев механизма.
3.2.1. Построение планов положений исследуемого механизма двухступенчатого компрессора.
Выбираем масштабный коэффициент
длин 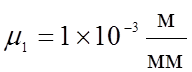 и рассчитываем чертежные размеры
звеньев (табл. 3.2).
и рассчитываем чертежные размеры
звеньев (табл. 3.2).
Т а б л и ц а 3.2.
Чертежные размеры звеньев.
|
О1А, мм |
О2В, мм |
ВС, мм |
BS4, мм |
О2S3, мм |
Y, мм |
H, мм |
|
50 |
125 |
500 |
200 |
25 |
8 |
250 |
Строим план положений механизма (приложение, лист 1).
3.3 Кинематическое исследование машин и механизмов
аналитическим методом.
3.2.2. Кинематическое исследование механизма аналитическим методом.
Для определения кинематических характеристик механизма применим метод замкнутых векторных контуров.
1. Рисуем во втором промежуточном положении структурную схему исследуемого механизма.
2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.
3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.
4. Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры: O1AO2, O2BC (рис.3.2)
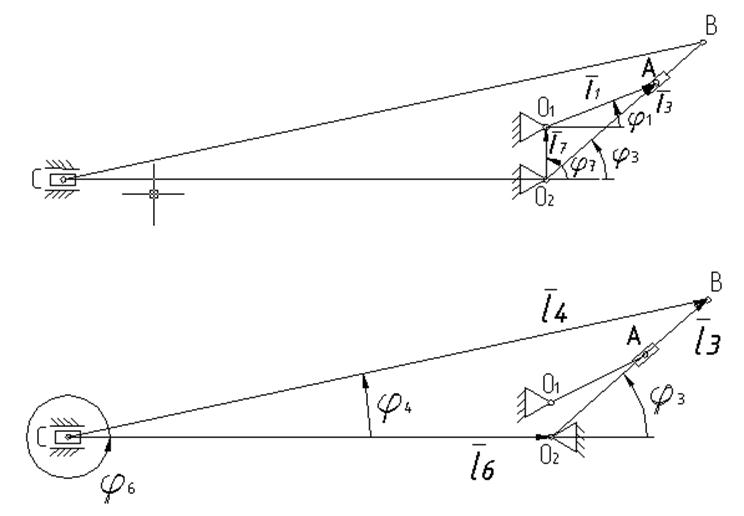
Рис. 3.2. Построение контуров
5. Записываем уравнение замкнутости первого контура в векторной форме. Все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие - со знаком «–»:
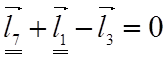 (3.1)
(3.1)
Уравнению (3.1) соответствуют два уравнения проекций на оси координат:
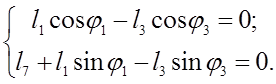 (3.2)
(3.2)
Среди величин, входящих в уравнение (3.2) переменными являются углы
![]() ,
, ![]() и
длина l3. Угол
и
длина l3. Угол ![]() является обобщенной координатой
механизма. Решив уравнения (3.2) получим:
является обобщенной координатой
механизма. Решив уравнения (3.2) получим:
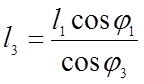 ;
(3.3)
;
(3.3)
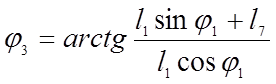 (3.4)
(3.4)
Рассмотрим контур O2BC,
уравнение замкнутости которого имеет вид: 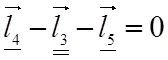
Спроецировав это векторное уравнение на оси координат получим:
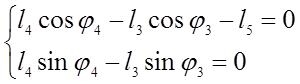 (3.5)
(3.5)
Решив эту систему найдем ![]() и
и ![]() :
:
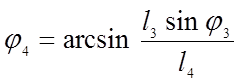 (3.6)
(3.6)
![]() (3.7)
(3.7)
.
Для нахождения положений точек ![]() и
и ![]() записываем
уравнения замкнутости контуров O2O1S3 и O2S4B (рис. 3.3):
записываем
уравнения замкнутости контуров O2O1S3 и O2S4B (рис. 3.3):
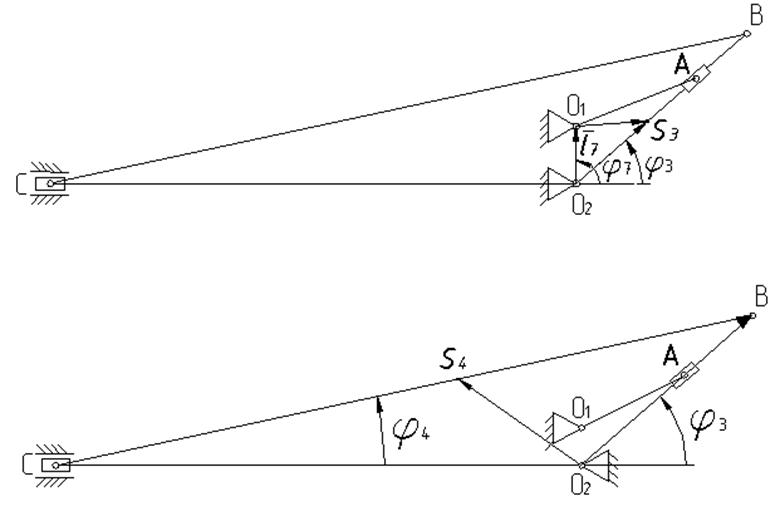
Рис. 3.3. Построение контуров
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
Из уравнений (3.8) и (3.9) находим координаты центров масс звеньев 3 и 4:
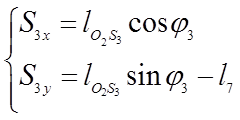 (3.10)
(3.10)
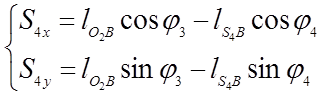 (3.11)
(3.11)
Результаты расчетов приводим в табл.3.3.
Т а б л и ц а (3.3)
|
φ1° |
φ3° |
φ4° |
l3, м |
l5, м |
s3x, м |
s3y, м |
s4x, м |
s4y, м |
|
351 |
0,207 |
0,052 |
0,049 |
0,37500061 |
0,025 |
-0,01 |
-0,08 |
3E-04 |
|
11 |
19,67 |
4,826 |
0,052 |
0,3805182 |
0,024 |
4E-04 |
-0,08 |
0,025 |
|
21 |
29,04 |
6,971 |
0,053 |
0,38702037 |
0,022 |
0,004 |
-0,09 |
0,036 |
|
31 |
38,22 |
8,898 |
0,055 |
0,39577923 |
0,02 |
0,007 |
-0,1 |
0,046 |
|
41 |
47,24 |
10,58 |
0,056 |
0,40663456 |
0,017 |
0,01 |
-0,11 |
0,055 |
|
51 |
56,12 |
11,98 |
0,056 |
0,41942623 |
0,014 |
0,013 |
-0,13 |
0,062 |
|
61 |
64,89 |
13,08 |
0,057 |
0,43398053 |
0,011 |
0,015 |
-0,14 |
0,068 |
|
71 |
73,59 |
13,88 |
0,058 |
0,45009678 |
0,007 |
0,016 |
-0,16 |
0,072 |
|
81 |
82,24 |
14,34 |
0,058 |
0,46753528 |
0,003 |
0,017 |
-0,18 |
0,074 |
|
91 |
-89,1 |
-14,5 |
-0,06 |
0,48224589 |
4E-04 |
-0,03 |
-0,19 |
-0,07 |
|
101 |
-80,5 |
-14,3 |
-0,06 |
0,46395489 |
0,004 |
-0,03 |
-0,17 |
-0,07 |
|
111 |
-71,9 |
-13,7 |
-0,06 |
0,44675943 |
0,008 |
-0,03 |
-0,16 |
-0,07 |
|
121 |
-63,1 |
-12,9 |
-0,06 |
0,4309378 |
0,011 |
-0,03 |
-0,14 |
-0,07 |
|
131 |
-54,4 |
-11,7 |
-0,06 |
0,41672102 |
0,015 |
-0,03 |
-0,12 |
-0,06 |
|
141 |
-45,4 |
-10,3 |
-0,06 |
0,40430335 |
0,018 |
-0,03 |
-0,11 |
-0,05 |
|
151 |
-36,4 |
-8,53 |
-0,05 |
0,3938547 |
0,02 |
-0,02 |
-0,1 |
-0,04 |
|
161 |
-27,2 |
-6,56 |
-0,05 |
0,38553412 |
0,022 |
-0,02 |
-0,09 |
-0,03 |
|
171 |
-17,8 |
-4,37 |
-0,05 |
0,37950346 |
0,024 |
-0,02 |
-0,08 |
-0,02 |
|
181 |
-8,11 |
-2,02 |
-0,05 |
0,37593997 |
0,025 |
-0,01 |
-0,08 |
-0,01 |
|
189 |
-0,21 |
-0,05 |
-0,05 |
0,37500061 |
0,025 |
-0,01 |
-0,08 |
-0 |
|
191 |
1,798 |
0,449 |
-0,05 |
0,37504614 |
0,025 |
-0,01 |
-0,08 |
0,002 |
|
201 |
12 |
2,978 |
-0,05 |
0,37705425 |
0,024 |
-0 |
-0,08 |
0,016 |
|
211 |
22,5 |
5,49 |
-0,05 |
0,38222112 |
0,023 |
0,002 |
-0,08 |
0,029 |
|
221 |
33,32 |
7,893 |
-0,05 |
0,39080732 |
0,021 |
0,006 |
-0,09 |
0,041 |
|
231 |
44,44 |
10,08 |
-0,04 |
0,40303311 |
0,018 |
0,01 |
-0,11 |
0,053 |
|
241 |
55,85 |
11,94 |
-0,04 |
0,41900607 |
0,014 |
0,013 |
-0,13 |
0,062 |
|
251 |
67,49 |
13,35 |
-0,04 |
0,43862288 |
0,01 |
0,015 |
-0,15 |
0,069 |
|
261 |
79,3 |
14,22 |
-0,04 |
0,46146495 |
0,005 |
0,017 |
-0,17 |
0,074 |
|
271 |
-88,8 |
-14,5 |
0,042 |
0,48153289 |
5E-04 |
-0,03 |
-0,19 |
-0,07 |
|
281 |
-76,9 |
-14,1 |
0,042 |
0,45667137 |
0,006 |
-0,03 |
-0,17 |
-0,07 |
|
291 |
-65,1 |
-13,1 |
0,043 |
0,43442281 |
0,011 |
-0,03 |
-0,14 |
-0,07 |
|
301 |
-53,5 |
-11,6 |
0,043 |
0,41551275 |
0,015 |
-0,03 |
-0,12 |
-0,06 |
|
311 |
-42,2 |
-9,67 |
0,044 |
0,40028927 |
0,019 |
-0,02 |
-0,1 |
-0,05 |
|
321 |
-31,1 |
-7,43 |
0,045 |
0,38880488 |
0,021 |
-0,02 |
-0,09 |
-0,04 |
|
331 |
-20,4 |
-4,99 |
0,047 |
0,38092232 |
0,023 |
-0,02 |
-0,08 |
-0,03 |
|
341 |
-9,93 |
-2,47 |
0,048 |
0,37640839 |
0,025 |
-0,01 |
-0,08 |
-0,01 |
|
351 |
0,207 |
0,052 |
0,049 |
0,37500061 |
0,025 |
-0,01 |
-0,08 |
3E-04 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.