Кинематический анализ рычажного механизма

Раздел 2. Кинематический анализ рычажного механизма

2.1. Определение крайних положений механизма

Для кривошипно-ползунного механизма крайними будут такие положения (рис. 2.1), когда кривошип и шатун то вытягиваются (ОА_кВ_к), то складываются в одну линию (A_нОВ_н). Тогда φ_р и φ_х будут углами рабочего и холостого хода механизма, а углы φ_н и φ_к – начальным и конечным углами соответственно.

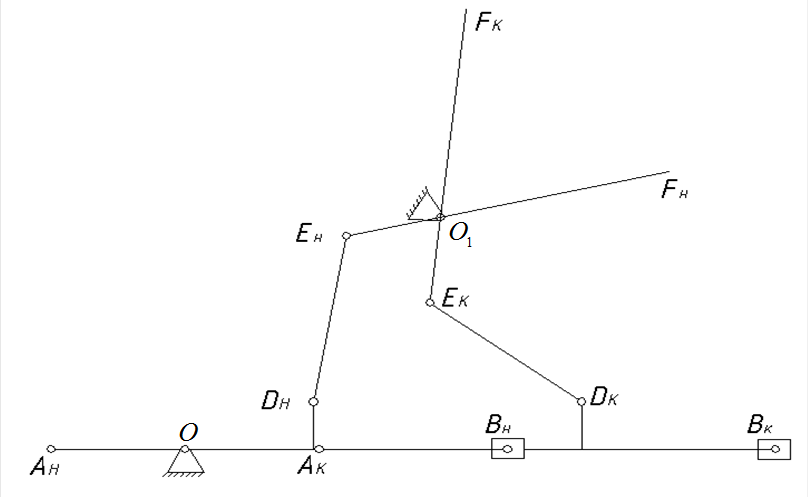
Рис. 2.1

Из построения видно:

2.2. Определение положений звеньев механизма

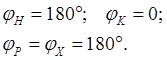
            Выбираем масштабный коэффициент длин m₁ = 0,005 м/мм и рассчитываем чертежные размеры звеньев (табл. 2.1).

Таблица 2.1

Чертежные размеры звеньев

Строим план механизма (Приложение 1).

2.3. Кинематическое исследование механизма аналитическим методом

Будем находить кинематические характеристики методом Зиновьева (метод замкнутых векторных контуров).

Структурную схему механизма располагаем в прямоугольной системе координат, начало которой помещаем в точку O₁. Рисуем структурную схему механизма в пятом положении (рис. 2.2).

Определяем угол j₁:

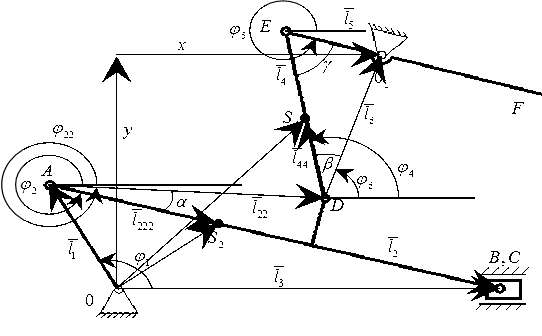
Рис. 2.2

Записываем уравнение замкнутости контура ОАВО в векторном виде:

                                                                                                                                                     (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат:

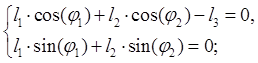                                                                                                                  (2.2)

Решаем систему (2.2) :

                          

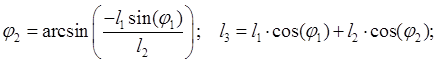
Определим угол :

        

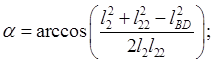
Записываем уравнение замкнутости контура OABDEO₁O в векторном виде:

                                                                                                                             (2.3)

Уравнению (2.3) соответствуют два уравнения проекций на оси координат:

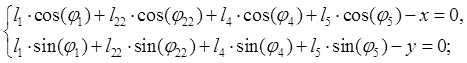                                                                (2.4)

Для решения системы (2.4) введем вспомогательный вектор l₆:

                                                                                                                                     (2.5)

Уравнению (2.5) соответствуют два уравнения проекций на оси координат:

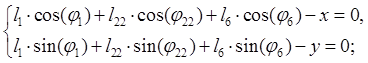                                                                                        (2.6)

Решаем систему (2.6):

       

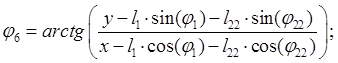
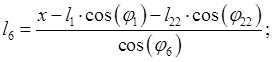
Определим угол :

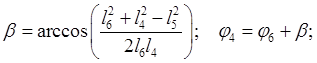
Определим угол :

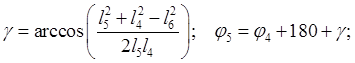
Для нахождения положений точек S₂ и S₄ записываем уравнение замкнутости контуров ОАS₂O и ОАDS₄O:

                                                                                                                          (2.7)

                                                                                                                   (2.8)

Из уравнений (2.9) и (2.10) находим координаты центров масс звеньев 3 и 2:

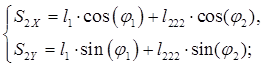                                                                                            (2.9)

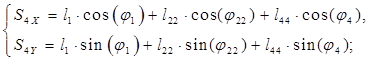                                                                (2.10)

Вычисления производим в MathCAD, результаты сводим в таблицу 2.2.

Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в табл. 2.2.

Таблица 2.2

Результаты расчета положений звеньев

Величина	j10	j20	j220	l3,м	l6,м	j60	j40	j50
Графически	30	8,474	5,789	1,182	0,437	128,129	156,869	67,66
Аналитически	30	8,474	5,789	1,182	0,437	128,129	156,869	67,66
Отклонение, D %	0	0	0	0	0	0	0	0

Найдём аналоги скоростей и ускорений.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем

Дифференцируем по обобщенной координате уравнение (2.2)

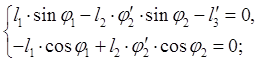                                                                                           (2.11)

;     ;

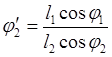Вычисления производим в MathCAD, результаты сводим в таблицу 2.3.

После дифференцирования уравнения (2.4) получим:

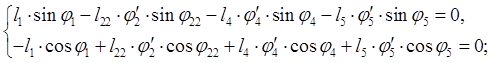                                   (2.12)

В MathCAD решаем систему (2.12) методом обратных матриц, находим  и .

Аналоги скоростей центров масс звеньев 2 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.9) и  (2.10):

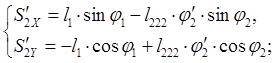                                                                                       (2.13)

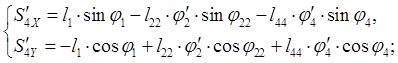                                                          (2.14)

Вычисляем системы (2.18), (2.19) в MathCAD и результаты сводим в таблицу 2.3.

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.11), (2.12).

После дифференцирования уравнений (2.11) получим:

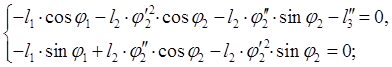                                                                                (2.15)

В MathCADрешаем систему (2.15), находим и.

После дифференцирования уравнений (2.12) получим:

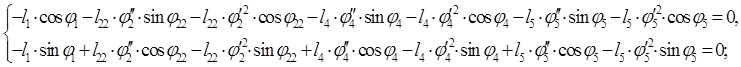 (2.16)

В MathCAD решаем систему (2.1), находим  и .

Аналоги ускорений центров масс звеньев 2 и 3 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.13) и  (2.14).

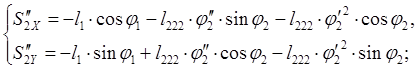                                                                              (2.17)

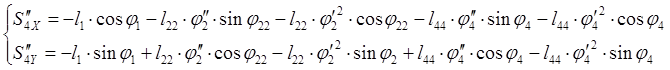                  (2.18)

Вычисляем системы (2.17), (2.18) в MathCAD и результаты сводим в таблицу 2.4.

2.4. Построение планов скоростей и ускорений

2.4.1. Определение аналогов скоростей исследуемого механизма графическим методом

Решение задачи графическим методом основано на построении плана скоростей для пятого положения механизма при j₁ = 30⁰ . Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁= -1 рад/с.

Построение плана скоростей:

1). находим скорость точки А:

                    

2). из полюса плана скоростей p откладываем отрезок pa  = 50 мм, изображающий вектор скорости точки А (рис. 2.3);

3). подсчитываем масштабный коэффициент скоростей: