Кинематическое исследование механизма аналитическим методом

3.1 Кинематическое исследование механизма аналитическим методом.

Используем метод замкнутых векторных контуров для определения линейных и угловых координат, скоростей и ускорений точек звеньев механизма.

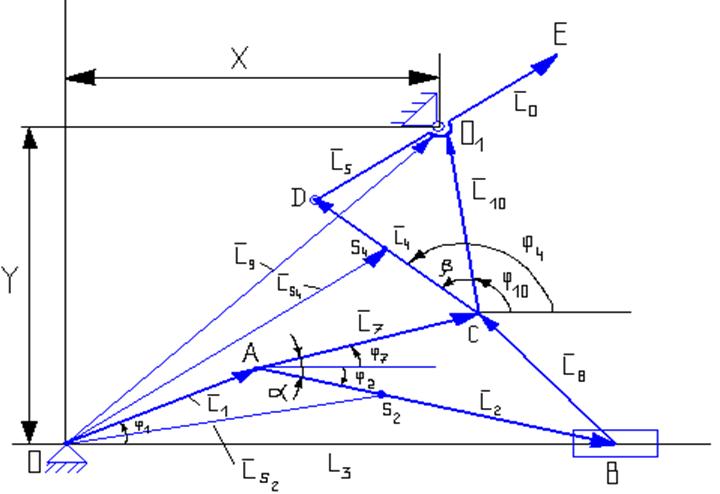
      Записываем уравнение замкнутости первого контура ОАBО. Для этого обходим его периметр в направлении вектора L1,причем все векторы, совпадающие с направлением обхода, ставятся со знаком ''+'' и не совпадающие – со знаком '' - '' :

                                                                        (3.1)

      Записываем уравнение для второго контура OACDO1O.

                                                      (3.2)

  

   Представим уравнение (3.1) в проекциях на оси координат:

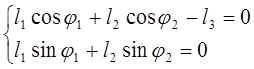                                                     (3.3)

Из уравнений (3.3) находим

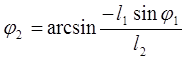                                                         (3.4)

                                                                                    (3.5)

Уравнение замкнутости второго контура в проекциях:

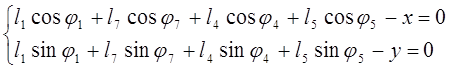                                    (3.6)

Т.к. уравнение (3.6)  сложны для решения введём дополнительный вектор  и запишем два векторных уравнения:

                                                                                             (3.7)

                                                                                                    (3.8)

В проекциях (3.7):

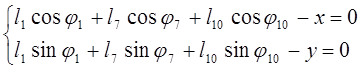                                                     (3.9)

Из треугольника ACB определяем угол :

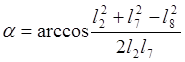                                                                                       (3.10)

                                                                                                          (3.11)

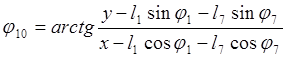                                                                    (3.12)

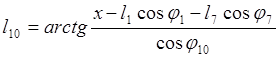                                                                     (3.13)

(3.8) в проекциях:

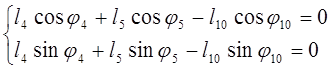                                                          (3.14)

из треугольника CDO1 определяем угол :

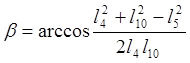                                                                                      (3.15)

                                                                                                      (3.16)

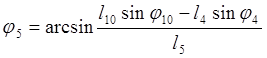                                                                         (3.17)

координаты центров масс:

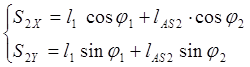                                                                                  (3.18)

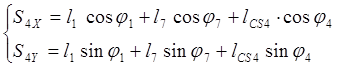                                                            (3.19)

С целью проверки правильности полученных выражений производим расчет по формулам (2.3) (2.4) (2.10) (2.11) (2.12) (2.13) (2.15) (2.16) (2.17) (2.18) (2.19)

для 5 положения кривошипа ОА:

т.е. , считая

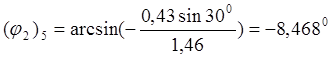
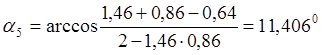
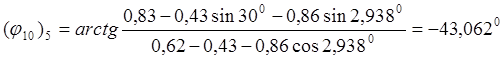
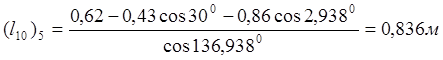
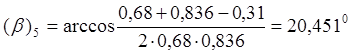
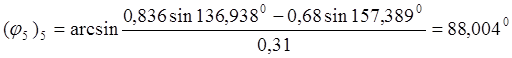
Результаты расчёта положений звеньев:             

Таблица 3.1.

Величина
Графически		-8,0	1,82	157	87
Аналитически		-8,468	1,816				0,151	0,917	0,390
Отклонение,		5,8	0,22	0,25	1,1

 

Определяем аналоги скоростей. Принимаем (по часовой стрелки)

Дифференцируем по обобщённой координате уравнения (3.3):

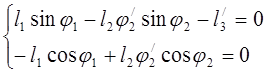                                                   (3.20)

Отсюда:

                                                                                     (3.22)

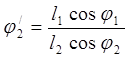                                                                                                  (3,21)

Дифференцируем уравнения (3.6): 

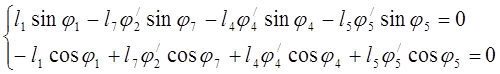                                  (3.23)

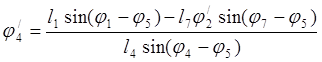                                                                         (3.24)

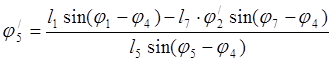                                                                       (3.25)

Дифференцируем (3.18) и (3.19):

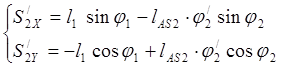                                                                                 (3.26)

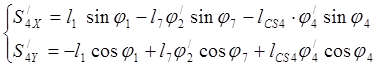                                                              (3.27)

Для положения 5:

             

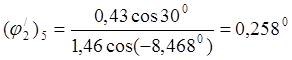
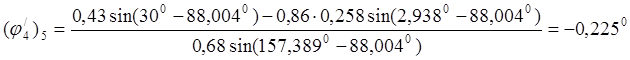
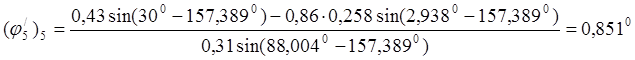
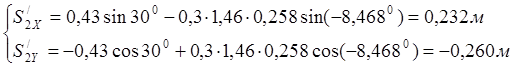
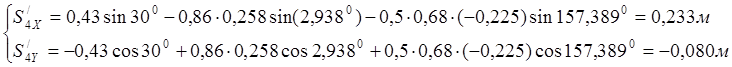
Определение аналогов ускорений основано на дифференцировании уравнений (3.20) (3.23) (3.26) (3.27)

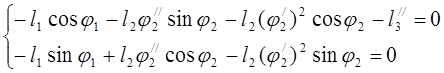                                                (3.28)

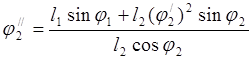                                                                                       (3.29)

                                                                (3.30)

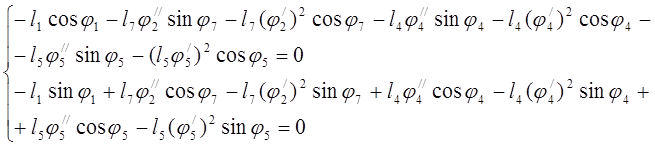        (3.31)

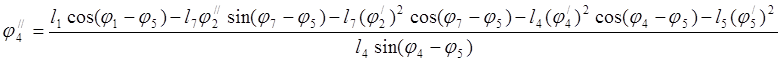
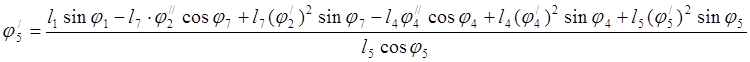
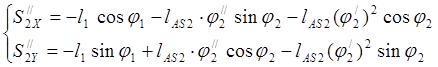                                                       (3.32)

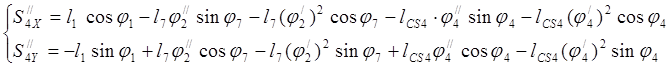         (3.33)

3.2. Определение аналогов скоростей механизма графическим методом.

1)Скорость точки :

;

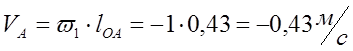2) из полюса плана скоростей p откладываем отрезок =100мм, изображающий вектор скорости точки ;

3) подсчитываем масштабный коэффициент скоростей:

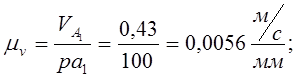
4) скорость точки B:

                         уравнение решаем графически.

                                       

Через точку проводим линию, перпендикулярную AB, а через точку p – прямую  до пересечения первой.

5) Скорость точки С определяем, используя теорему подобия

подобен ,

на отрезке ab строим подобный звену 2 (ABC):

6) Скорость точки D:

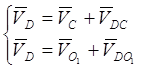                       Систему решаем графически

Из точки С проводим прямую, перпендикулярную DC

И точки p проводим прямую, перпендикулярную  до пересечении с первой – ставим точку d

7) Скорость точки E: из принципа подобия

                      

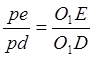
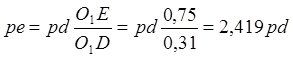
8) Положения точек  и  так же находим по теореме подобия.

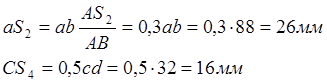
 и  изображают

9) из плана скоростей находим:

 

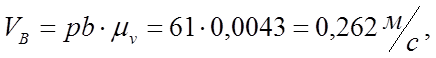
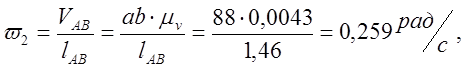
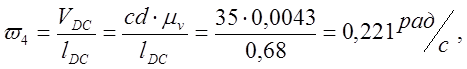
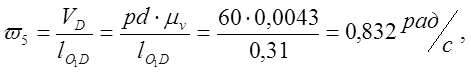
Определяем аналоги линейных и угловых скоростей:

                 

                   

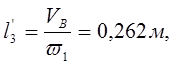
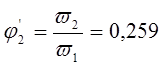
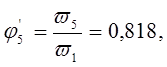
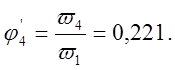
Таблица 3.1.

Величина
Из плана скоростей	0,259	0,262	0,221	0,832	-	-	-	-
Аналити-чески	0,258	0,270	-0,225	0,851	0,232	-0,260	0,233	-0,080
Погрешность	0,4	2,9	1,8	2,2	-	-	-	-

Направления  указаны на чертеже.

3.3. Определение аналогов ускорений механизма графическим методом.

1)  Ускорение точки A:

 

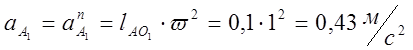
2)Из точки - полюса плана ускорений – откладываем вектор , изображающий ускорение точки  в виде отрезка

2)  Подсчитываем масштабный коэффициент ускорений

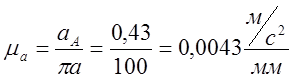
3)  Ускорение точки B

                         ,                                    

                                      

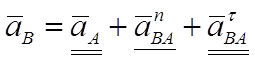Решаем графически нормальное ускорение

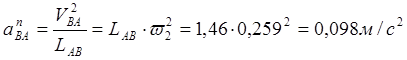
Из точки а откладываем отрезок 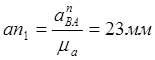 параллельно в направлении от В к А.

Через  проводим прямую перпендикулярную АВ

Через  проводим прямую до пересечения с последней, отсюда точка b.

4)  Ускорение точки С:

Из теоремы подобия строим на ab треугольник ABC, подобный треугольнику ABC.

               

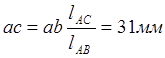
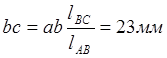
5)  Ускорение точки D:

                                                                    

                                                             

                        

                                                    

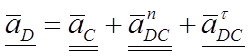
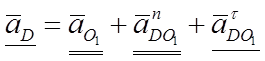
Решаем систему графическим методом

Определяем нормальные ускорения:

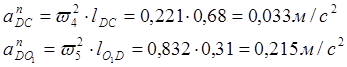
Отразим, изобразим эти ускорения:

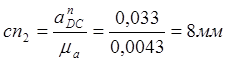
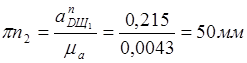
Из точки С откладываем  параллельно  (От D к С)

Через проводим прямую, перпендикулярную CD.

Из точки  откладываем  параллельно  (от D к )

Через проводим прямую, перпендикулярную

На пересечении перпендикуляров – точка d.

6)  Ускорения точек E определяем, используя теорему подобия

7)  Из плана ускорений получаем:

     

          

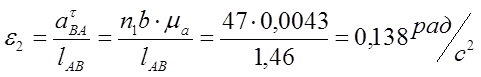
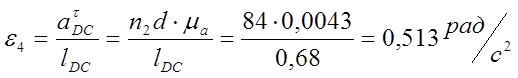
Аналоги линейных и угловых ускорений:

                                        

                           

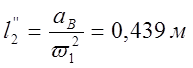
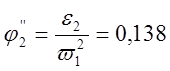
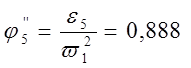
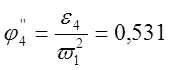
Направления показаны на чертеже.

Таблица 3.2.

Величина
Из плана скоростей	0,138	-0,439	-0,531	-0,888	-	-	-	-
Аналити-чески	0,139	-0,438	-0,552	-0,913	-0,392	-0,138	-0,352	0,058
Погрешность	1,7	0,14	3,7	2,7	-	-	-	-