3.1 Кинематическое исследование механизма аналитическим методом.
Используем метод замкнутых векторных контуров для определения линейных и угловых координат, скоростей и ускорений точек звеньев механизма.
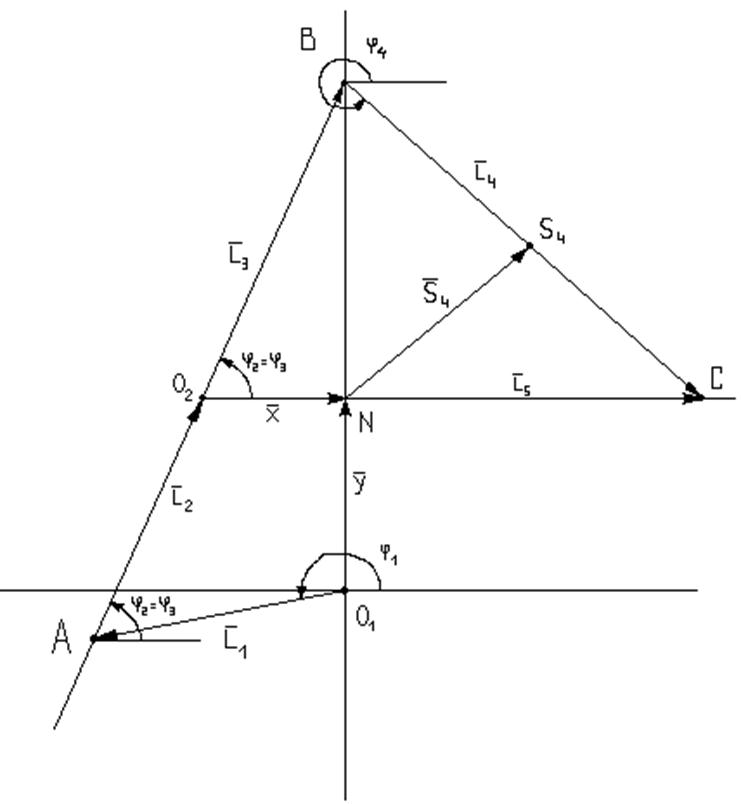
Записываем уравнение замкнутости первого контура О1АО2N. Для этого обходим его периметр в направлении вектора L1,причем все векторы, совпадающие с направлением обхода, ставятся со знаком ''+'' и не совпадающие – со знаком '' - '' :
![]()
![]()
![]() (3.1)
(3.1)
Записываем уравнение для второго контура О2ВСN.
![]()
![]() (3.2)
(3.2)
![]()
![]() Представим уравнение
(3.1) в проекциях на оси координат:
Представим уравнение
(3.1) в проекциях на оси координат:
![]()
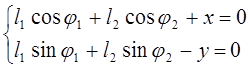 (3.3)
(3.3)
Из уравнений (3.3) находим угол
наклона вектора ![]()
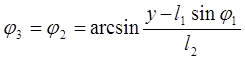 +k
+k![]() (3.4)
(3.4)
и его модуль
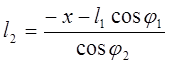 (3.5)
(3.5)
где к=0,1,2,3,…
Угол ![]() и
модуль вектора
и
модуль вектора ![]() находим из уравнения (3.2),
записав его в развернутом виде:
находим из уравнения (3.2),
записав его в развернутом виде:
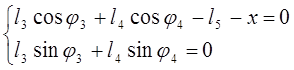 (3.6)
(3.6)
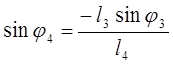
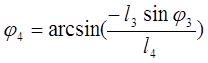 (3.7)
(3.7)
![]() (3.8)
(3.8)
Находим координаты центров масс звеньев 4 и 5.
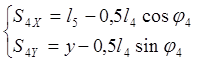 (3.9)
(3.9) 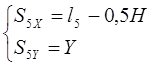 (3.10)
(3.10) 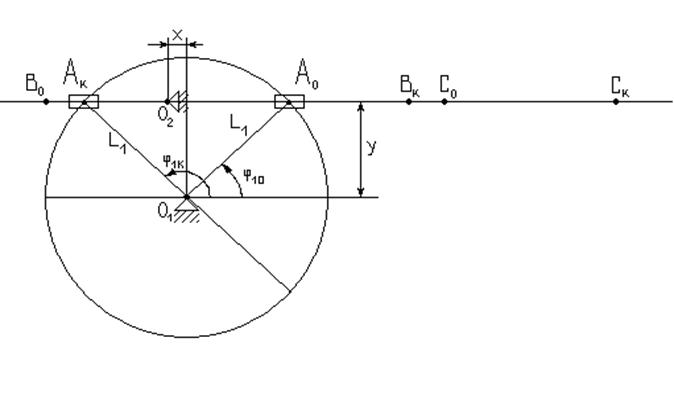
Находим крайние положения механизма.
![]()
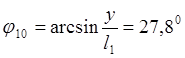
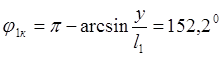
За расчётное принимается положение 5 кривошипа O1A.
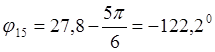
Найдём значения линейных и угловых координат для положения 5 кривошипа.
Для положения 5: (при ![]() )
)
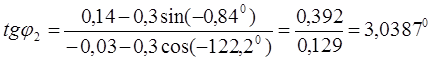
![]()
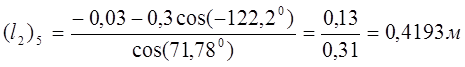
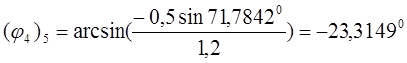
![]()
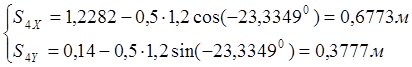
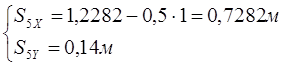
Таблица 3.1.
|
Величина |
|
|
|
|
|
|
Графически |
-122 |
70,5 |
-23,5 |
0,42 |
1,23 |
|
Аналитически |
|
|
|
|
|
|
Отклонение,
|
0,16 |
1,7 |
0,8 |
0,16 |
0,14 |
Для определения аналогов скоростей механизма дифференцируем уравнения (3.3)
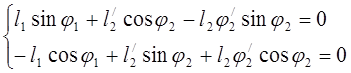 (3.11)
(3.11)
Находим аналоги скоростей ![]() ,
, ![]()
![]()
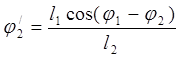
Дифференцируем уравнения (3.6)
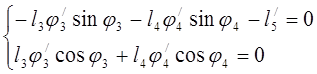 (3.12)
(3.12)
![]()
Определяем аналоги скоростей ![]() и
и ![]()
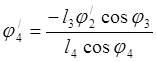
![]()
Определяем аналоги скоростей центров масс звеньев
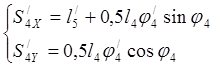 (3.13)
(3.13)
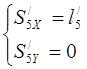 (3.14)
(3.14)
Для определения аналогов ускорений дифференцируем уравнения (3.11)
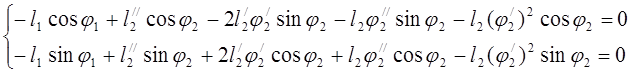 (3.15)
(3.15)
Определяем аналоги ускорений ![]() и
и ![]()
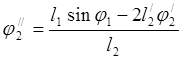
![]()
Дифференцируем уравнения (3.12)
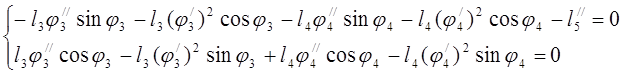 (3.16)
(3.16)
Определяем аналоги ускорений ![]() и
и ![]()
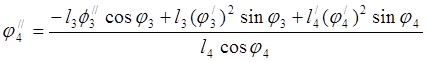
![]()
Аналоги ускорений центров масс определяем, дифференцируя уравнения (3.13), (3.14)
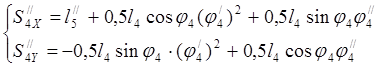 (3.17)
(3.17)
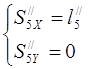 (3.18)
(3.18)
3.2. Определение аналогов скоростей механизма графическим методом.
1)Скорость точки ![]() звена 1:
звена 1:
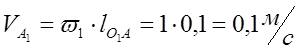 ;
;
2) из полюса плана скоростей p
откладываем отрезок ![]() =100мм, изображающий вектор
скорости точки
=100мм, изображающий вектор
скорости точки ![]() ;
;
3) подсчитываем масштабный коэффициент скоростей:
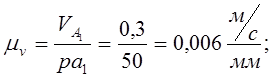
4) скорость точки ![]() , которая
является общей для звеньев 2 и 3, находим, раскладывая движение на переносное
(вращательное) вместе с точкой
, которая
является общей для звеньев 2 и 3, находим, раскладывая движение на переносное
(вращательное) вместе с точкой ![]() и относительное
(поступательное) по отношению к точке
и относительное
(поступательное) по отношению к точке ![]() .
.
![]() (3.19)
(3.19)
![]()
![]()
Через точку ![]() проводим
линию, параллельную
проводим
линию, параллельную ![]() , а через полюс – линию,
перпендикулярную
, а через полюс – линию,
перпендикулярную ![]() до пересечения их в точке
до пересечения их в точке ![]() .
.
5) Скорость точки ![]() звена 3
определяем, используя теорему подобия
звена 3
определяем, используя теорему подобия
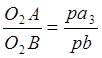 ,
,
откуда
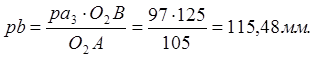
Отрезок ![]() откладываем от
полюса
откладываем от
полюса ![]() на продолжении отрезка
на продолжении отрезка ![]() .
.
6) Скорость точки ![]() находим согласно
векторному уравнению
находим согласно
векторному уравнению
![]() (3.20)
(3.20)
![]()
![]()
Через точку b проводим прямую,
перпендикулярную ![]() , а из полюса
, а из полюса ![]() прямую, параллельную
прямую, параллельную ![]() , до пересечения их в точке
, до пересечения их в точке ![]() .
.
7) положения точек ![]() и
и
![]() на плане скоростей находим,
воспользовавшись теоремой подобия:
на плане скоростей находим,
воспользовавшись теоремой подобия:
![]()
![]()
![]()
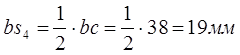 .
.
8) из плана скоростей находим:
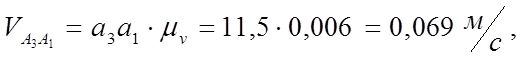
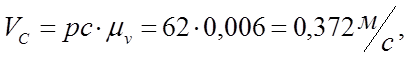
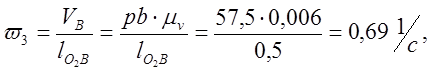
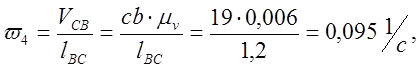
Определяем аналоги линейных и угловых скоростей:
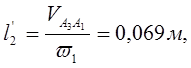
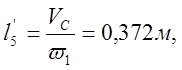
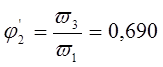
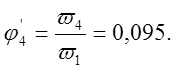
Таблица 3.1.
|
Величина |
|
|
|
|
|
|
|
|
|
Из плана скоростей |
0,690 |
0,069 |
0,095 |
0,372 |
- |
- |
- |
- |
|
Аналити-чески |
-0,695 |
0,068 |
0,092 |
0,376 |
0,348 |
0,054 |
0,376 |
0 |
|
Погрешность |
0,7 |
1,4 |
3,2 |
1,06 |
- |
- |
- |
- |
3.3. Определение аналогов ускорений механизма графическим методом.
1) Ускорение
точки ![]() , принадлежащей первому звену.
, принадлежащей первому звену.
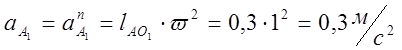
2)Из точки ![]() - полюса плана ускорений –
откладываем вектор , изображающий ускорение точки
- полюса плана ускорений –
откладываем вектор , изображающий ускорение точки ![]() в
виде отрезка
в
виде отрезка ![]()
2) Подсчитываем масштабный коэффициент ускорений
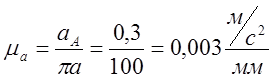
3) Ускорение
точки ![]() находим из уравнения
находим из уравнения
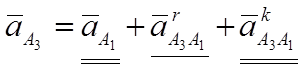 ,
(3.21)
,
(3.21)
![]()
![]()
![]()
где ![]() - относительное ускорение
точки
- относительное ускорение
точки ![]() относительно
относительно ![]() ,
,
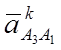 - кориолисово
ускорение.
- кориолисово
ускорение.
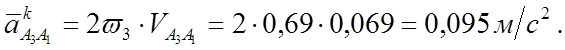
Отрезок, изображающий в миллиметрах вектор 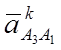 ,
,
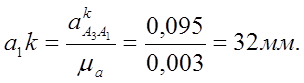
Направление кориолисова ускорения определяется поворотом
относительной скорости ![]() на
на ![]() по
направлению переносной угловой скорости
по
направлению переносной угловой скорости ![]() .
.
С другой стороны ускорение точки ![]() :
:
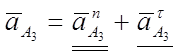 (3.22)
(3.22)
![]()
![]()
![]() - нормальное ускорение
точки
- нормальное ускорение
точки ![]() ,
,
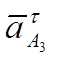 -тангенциальное
ускорение точки
-тангенциальное
ускорение точки ![]() .
.
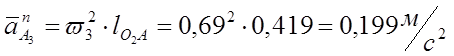
Отрезок, изображающий в миллиметрах ![]()
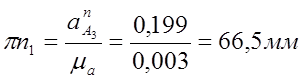
Из точки ![]() откладываем
отрезок
откладываем
отрезок ![]() , изображающий кориолисово ускорение.
, изображающий кориолисово ускорение.
Через точку ![]() проводим прямую,
параллельную
проводим прямую,
параллельную ![]() .
.
Из точки ![]() откладываем
отрезок
откладываем
отрезок ![]() , параллельно
, параллельно ![]() ,
через точку
,
через точку ![]() проводим прямую, перпендикулярную
проводим прямую, перпендикулярную ![]() до пересечения с предыдущей прямой в
точке
до пересечения с предыдущей прямой в
точке ![]() .
.
4) Для
расчета ускорения точки ![]() используем
теорему подобия:
используем
теорему подобия:
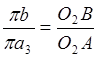 , откуда находим
, откуда находим 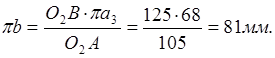
5) Ускорение точки С определяем согласно векторному уравнению.
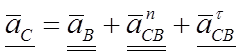 (3.23)
(3.23)
![]()
![]()
![]()
![]()
Нормальное ускорение точки С относительно В:
![]() ,
,
отрезок, изображающий ![]() :
:
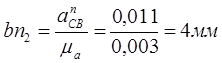
Из точки ![]() строим вектор
строим вектор ![]() параллельно BC
(от C к B), через точку
параллельно BC
(от C к B), через точку ![]() проводим прямую, перпендикулярную
проводим прямую, перпендикулярную ![]() . Через точку
. Через точку ![]() проводим
прямую, параллельную
проводим
прямую, параллельную ![]() до пересечения с предыдущей
в точке с.
до пересечения с предыдущей
в точке с.
6) Ускорения
точек ![]() ,
, ![]() определяем,
используя теорему подобия.
определяем,
используя теорему подобия.
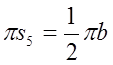 ,
,
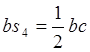 .
.
7) Из плана ускорений получаем:
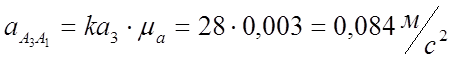
![]()
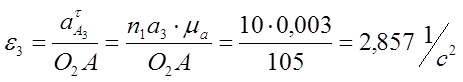
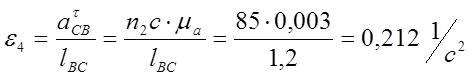
![]()
Аналоги линейных и угловых ускорений:
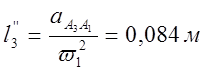
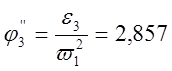
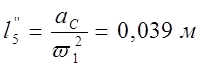
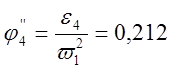
Таблица 3.2.
|
Величина |
|
|
|
|
|
|
|
|
|
Из плана скоростей |
2,857 |
0,084 |
0,212 |
0,039 |
- |
- |
- |
- |
|
Аналити-чески |
2,850 |
0,087 |
0,208 |
0,040 |
-0,006 |
-0,120 |
0,040 |
0 |
|
Погрешность |
0,2 |
3,4 |
1,9 |
2,5 |
- |
- |
- |
- |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.