Синтез планетарной передачи состоит в подборе чисел зубьев колес по заданной схеме, а также определение передаточного отношения для подобранных чисел зубьев и построение плана скоростей.
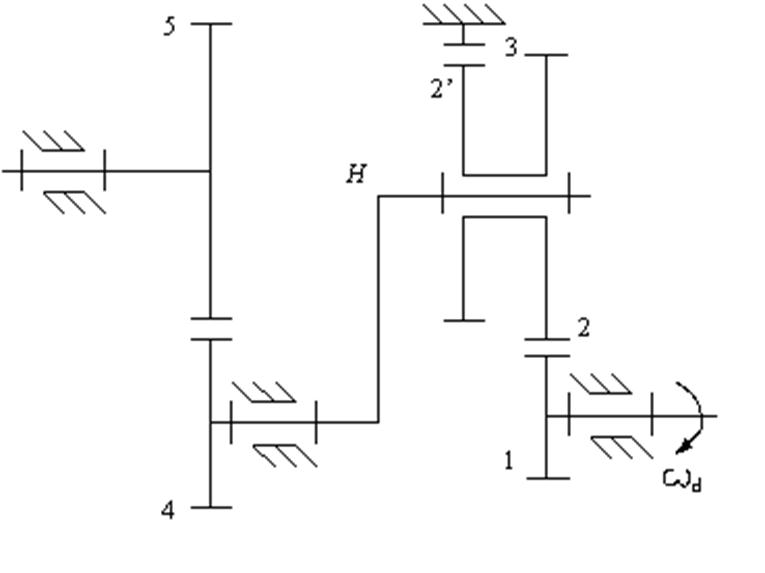
Рис.4.1. Структурная схема зубчатого механизма.
4.1.Подбор числа зубьев. проводим по методу Гавриленко.
Для колеса с внешним зацеплением число
зубьев должно быть ![]() .
.
Для колеса с внутренним
зацеплением ![]() .
.
Условие зацепления по передаточному отношению:
Условие соосности:
![]() (4.1)
(4.1)
Уравнение заданного передаточного отношения:
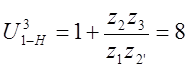 (4.2)
(4.2)
Уравнение сборки:
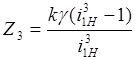 (4.3)
(4.3)
Условия соседства:
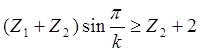 ,
,
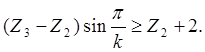 (4.4)
(4.4)
Находим значения![]() , лежащие в заданных пределах от 51
до 150, при которых
, лежащие в заданных пределах от 51
до 150, при которых ![]() будет целым числом
будет целым числом 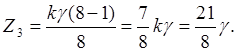 (4.5)
(4.5)
В таблице 4.1 приведены числа
зубьев колеса 3 при различных значениях K и ![]() .
.
Таблица 4.1
|
Число сателлитов К |
Значение |
Числа зубьев колеса 3 |
|
3 |
24 |
63 |
|
32 |
84 |
|
|
40 |
105 |
|
|
48 |
126 |
|
|
56 |
147 |
Из уравнений (4.1) и (4.2) выводим формулу:
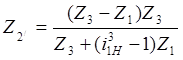 (4.6)
(4.6)
Подставляя в полученную формулу
найденные значения Z1 и задаваясь значениями
![]() , находим Z2.
, находим Z2.
В таблице 4.2 приведены значения Z1 и Z2 , при которых Z2 получаются целыми.
Таблица 4.2
|
Номер варианта |
Z1 |
Z2 |
Z3 |
|
|
1 |
18 |
30 |
15 |
63 |
|
2 |
18 |
54 |
54 |
126 |
|
3 |
54 |
54 |
18 |
126 |
|
4 |
24 |
56 |
40 |
120 |
Выбираем вариант, при котором
числа зубьев наименьшие: ![]()
1. Находим
начальные диаметры колес планетарной передачи и вычерчиваем
кинематическую схему механизма, приняв масштабный коэффициент ![]() 10 мм/мм (рис. 4.1,а).
10 мм/мм (рис. 4.1,а).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.