5. СИНТЕЗ ПЛАНЕТАРНОЙ ПЕРЕДАЧИ
Синтез планетарной передачи состоит в подборе чисел зубьев колес и числа сателлитов по заданной схеме и передаточному отношению.
При решении задачи используются условия соосности, сборки и соседства. Кроме того, числа зубьев колес должны находиться в пределах от 17 до 150.
В соответствии с данными [1] для заданной схемы записываем три уравнения и два неравенства:
уравнение заданного передаточного отношения
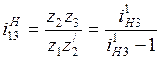 ,
(5.1)
,
(5.1)
уравнение соосности колес 1 и 3
![]() ,
(5.2)
,
(5.2)
уравнение сборки
![]() ,
(5.3)
,
(5.3)
условие соседства
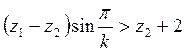 ,
,
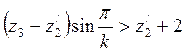 (5.4)
(5.4)
В уравнениях обозначено: ![]() ,
, ![]() ,
, ![]() ,
, ![]() -
числа зубьев колес 1, 2, 2/, 3 соответственно, k – число сателлитов,
-
числа зубьев колес 1, 2, 2/, 3 соответственно, k – число сателлитов, ![]() – целое число.
– целое число.
По уравнению (5.3)
находим значения ![]() , лежащие в пределах от 51
до 150, при которых
, лежащие в пределах от 51
до 150, при которых ![]() будет целым числом.
будет целым числом.
Число сателлитов k выбираем в пределах от 3 до 6.
В табл. 5.1 приведены
числа зубьев колеса 3 при различных значениях k и ![]() .
.
Из уравнений (5.1) и
(5.2) выразим ![]() через
через ![]() и
и ![]()
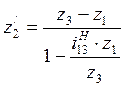
|
Число сателлитов k |
Значение |
Числа зубьев колеса 3 |
|
3 |
2 |
54 |
|
3 |
81 |
|
|
4 |
108 |
|
|
5 |
135 |
|
|
4 |
2 |
72 |
|
3 |
108 |
|
|
4 |
144 |
|
|
5 |
2 |
90 |
|
3 |
135 |
|
|
6 |
1 |
54 |
|
2 |
108 |
Подставляя в полученную
формулу найденные значения ![]() и задаваясь
значениями
и задаваясь
значениями ![]() , находим
, находим ![]() .
.
В табл. 5.2 приведены
значения ![]() и
и ![]() ,
при которых
,
при которых ![]() получаются целыми и удовлетворяют
условию соседства (5.4). Здесь же приведены значения
получаются целыми и удовлетворяют
условию соседства (5.4). Здесь же приведены значения ![]() ,
найденные по формуле
,
найденные по формуле ![]() и также удовлетворяющие
условию соседства (5.4).
и также удовлетворяющие
условию соседства (5.4).
|
Номер варианта |
Число сателлитов k |
Числа зубьев |
|||
|
|
|
|
|
||
|
1 |
3 |
84 |
21 |
18 |
81 |
|
2 |
112 |
28 |
24 |
108 |
|
|
3 |
114 |
38 |
32 |
108 |
|
|
4 |
138 |
23 |
20 |
135 |
|
|
5 |
140 |
35 |
30 |
135 |
|
|
6 |
144 |
54 |
45 |
135 |
|
|
7 |
145 |
58 |
48 |
135 |
|
|
8 |
4 |
112 |
28 |
24 |
108 |
|
9 |
114 |
38 |
32 |
108 |
|
|
10 |
5 |
138 |
23 |
20 |
135 |
|
11 |
140 |
35 |
30 |
135 |
|
|
12 |
5 |
144 |
54 |
45 |
135 |
|
13 |
6 |
112 |
28 |
24 |
108 |
Передаточное отношение зубчатого механизма определяем графическим методом для первого варианта.
Находим делительные диаметры зубчатых колес по формуле:
![]() (5.6)
(5.6)
Расчеты по формуле (5.6) приведены в табл. 5.3
|
Колесо |
1 |
2 |
2/ |
3 |
4 |
5 |
|
Делительный диаметр d, мм |
336 |
84 |
72 |
324 |
104 |
160 |
|
Модуль m |
4 |
8 |
||||
Вычерчиваем
кинематическую схему механизма (рис. 5.1), приняв масштабный коэффициент 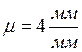 .
.
Строим план линейных скоростей.
Параллельно схеме механизма проводим вертикальную линию нулевых скоростей. Обозначаем проекции характерных точек механизма на линию нулевых скоростей одноименными прописными буквами латинского алфавита.
Из точки ![]() откладываем вектор произвольной
длины
откладываем вектор произвольной
длины ![]() , изображающий скорость точки
, изображающий скорость точки ![]() водило. Соединив точку
водило. Соединив точку ![]() с точкой
с точкой ![]() ,
получим линию Н распределения скоростей водило.
,
получим линию Н распределения скоростей водило.
Для сателлита 2 известны
скорости двух точек: точки ![]() и точки
и точки ![]() , скорость которой равна нулю. Прямая
2, соединяющая точки
, скорость которой равна нулю. Прямая
2, соединяющая точки ![]() и
и ![]() ,
является линией распределения скоростей в сателлитах 2 и 2/.
,
является линией распределения скоростей в сателлитах 2 и 2/.
На линии 2 лежит точка ![]() – конец вектора
– конец вектора ![]() , изображающего скорость точки
, изображающего скорость точки ![]() , общей для звеньев 2/ и
3. Соединив точку
, общей для звеньев 2/ и
3. Соединив точку ![]() с точкой
с точкой ![]() , получим линию 3 распределения
скоростей в колесе 3.
, получим линию 3 распределения
скоростей в колесе 3.
Вектор ![]() есть скорость точки
есть скорость точки ![]() колес 4 и 5, а отрезок
колес 4 и 5, а отрезок ![]() является линией распределения
скоростей колеса 5.
является линией распределения
скоростей колеса 5.
Строим план угловых скоростей.
На продолжении линии
нулевых скоростей откладываем отрезок ![]() произвольной
длины. Из точки
произвольной
длины. Из точки ![]() проводим прямые,
параллельные линиям
проводим прямые,
параллельные линиям ![]() , 2, 3 и 5 до пересечения
их в точках
, 2, 3 и 5 до пересечения
их в точках ![]() , 2, 3 и 5 с перпендикуляром к линии
, 2, 3 и 5 с перпендикуляром к линии ![]() соответственно.
соответственно.
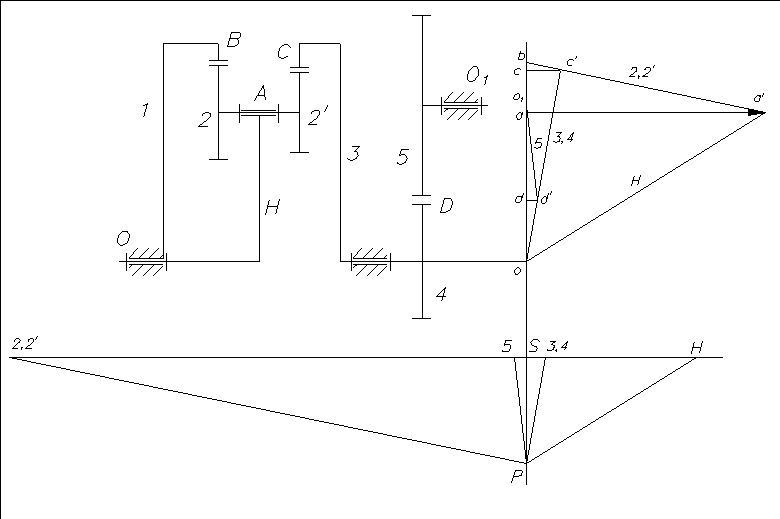
Передаточное отношение планетарной передачи определиться как:
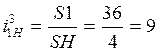
Передаточное отношение зубчатого механизма:
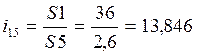
Причем передаточное
отношение зубчатого механизма будет отрицательным, т.к. отрезки ![]() и
и ![]() лежат
по разные стороны от точки
лежат
по разные стороны от точки ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.