Синтез планетарной передачи
Рис.
1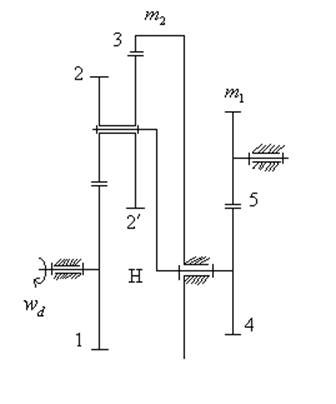
Дано:
![]() =107мм,
=107мм, ![]() =14,
=14, ![]() =28,
=28, ![]() =5,
=5, ![]() =7,
=7, ![]() =3,
=3, ![]() =3.
=3.
Решение:
1) В соответствии с данными таблицы 7.4 из [1] записываем три уравнения и два неравенства:
Уравнение заданного передаточного отношения
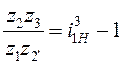 ,
(1)
,
(1)
Уравнение соосности колес ![]() 1 и
1 и ![]() 3
3
![]() ,
(2)
,
(2)
Уравнение сборки
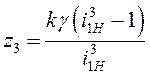 ,
(3)
,
(3)
Условие соседства
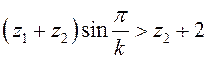 ,
, 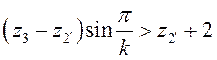 . (4)
. (4)
В уравнениях
обозначено: ![]() ,
, ![]() ,
, ![]() ,
, ![]() – числа зубьев
колес
– числа зубьев
колес ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно,
соответственно,
![]() – число сателлитов,
– число сателлитов, ![]() – целое число.
– целое число.
2) По уравнению (3) находим значения ![]() , лежащие в заданных пределах от 85 до
150 (табл. 7.4 из [1]), при которых
, лежащие в заданных пределах от 85 до
150 (табл. 7.4 из [1]), при которых ![]() будет целым
числом
будет целым
числом
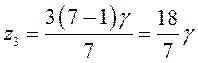 .
.
Число ![]() сателлитов равно 3.
сателлитов равно 3.
В таблице 1
приведены числа зубьев колеса при различных целых значениях ![]() .
.
Таблица 1
Числа зубьев колеса 3
|
Число
сателлитов |
Значение |
Числа зубьев
колеса |
|
3 |
35 |
90 |
|
42 |
108 |
|
|
49 |
126 |
|
|
56 |
144 |
3) Из уравнений (1) и (2) выразим ![]() через
через ![]() и
и ![]()
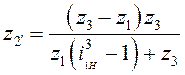 .
.
Подставляя в полученную
формулу найденные значения ![]() и задаваясь
значениями
и задаваясь
значениями ![]() , находим
, находим ![]() .
.
В табл. 2 приведены значения ![]() и
и ![]() , при которых
, при которых ![]() получаются целыми. Здесь же приведены
значения
получаются целыми. Здесь же приведены
значения ![]() , найденные по формуле
, найденные по формуле ![]() , полученной из уравнения соосности.
, полученной из уравнения соосности.
Таблица 2
Числа зубьев колес механизма
|
Номер варианта |
Числа зубьев |
|||
|
|
|
|
|
|
|
1 |
20 |
40 |
30 |
90 |
|
2 |
30 |
40 |
20 |
90 |
|
3 |
18 |
45 |
45 |
108 |
|
4 |
36 |
48 |
24 |
108 |
|
5 |
28 |
56 |
42 |
126 |
|
6 |
42 |
56 |
28 |
126 |
|
7 |
24 |
60 |
60 |
144 |
|
8 |
32 |
64 |
48 |
144 |
|
9 |
39 |
65 |
40 |
144 |
|
10 |
40 |
65 |
39 |
144 |
|
11 |
48 |
64 |
32 |
144 |
|
12 |
60 |
60 |
24 |
144 |
Из основных вариантов механизмов необходимо выбрать тот, который по результатам прочностного расчета будет иметь наименьшие габариты. Выбираем вариант 1.
Для проверки правильности
решения задачи определяем передаточное отношение зубчатого механизма. Общее передаточное
отношение зубчатого механизма равно произведению передаточных отношений
планетарной ступени и пары зубчатых колес ![]() и
и ![]() :
:
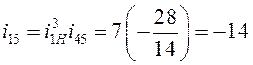 .
.
Знак минус
указывает на то, что колеса ![]() и
и ![]() вращаются в противоположных направлениях.
вращаются в противоположных направлениях.
Передаточное отношение зубчатого механизма определяем графическим методом.
1. Находим начальные диаметры колес планетарной передачи и вычерчиваем кинематическую схему механизма (рис. 2,а);
2. Строим план
линейных скоростей (рис. 2,б). Из точки ![]() откладываем
вектор
откладываем
вектор ![]() , изображающий скорость точки
, изображающий скорость точки ![]() колес
колес ![]() и
2. Соединив точку
и
2. Соединив точку ![]() с точкой О, получим линию
1 распределения скоростей колеса 1. Для сателлита
с точкой О, получим линию
1 распределения скоростей колеса 1. Для сателлита ![]() известны скорости двух точек: точки А и
точки С, скорость которой равна нулю. Прямая 2, соединяющая точки
известны скорости двух точек: точки А и
точки С, скорость которой равна нулю. Прямая 2, соединяющая точки ![]() и С, является линией распределения
скоростей на сателлите
и С, является линией распределения
скоростей на сателлите ![]() . На этой линии
лежит точка
. На этой линии
лежит точка ![]() – конец вектора
– конец вектора ![]() , изображающего скорость точки В, общей
для звеньев 2 и Н. Соединив точку
, изображающего скорость точки В, общей
для звеньев 2 и Н. Соединив точку ![]() с точкой О,
получим линию Н распределения скоростей в звене Н. Вектор
с точкой О,
получим линию Н распределения скоростей в звене Н. Вектор ![]() есть скорость точки D колеса 4 и 5, а
отрезок
есть скорость точки D колеса 4 и 5, а
отрезок ![]() является линией распределения
скоростей колеса 5.
является линией распределения
скоростей колеса 5.
3. Строим план угловых скоростей (рис. 2,в). На продолжении ОС откладываем отрезок PS произвольной длины. Из точки Р проводим прямые, параллельные линии 1, 2 Н и 5 до пересечения их в точках 1, 2, Н, 5 с перпендикуляром к линии PS;
В соответствии с 7.4.4.1 из [1] передаточное отношение планетарной передачи
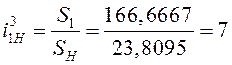 .
.
Тогда общее передаточное отношение зубчатого механизма
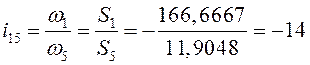 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.