Синтез кулачкового механизма с коромыслом. Вариант № 2

Синтез кулачкового механизма с коромыслом

1. В выражение аналога ускорения коромысла подставляем исходные данные:

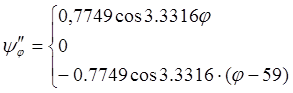
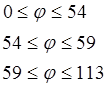                                                (1.1)

Проинтегрировав уравнение (1.1), получаем выражения для определения аналога скорости и угла поворота коромысла:

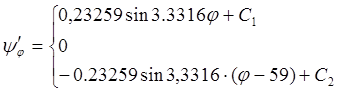
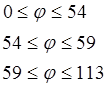                                        (1.2)

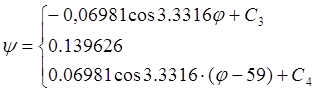
                                            (1.3)

Постоянные интегрирования определились из следующих начальных условий: при  , и при  ,

С1=0, С2=0.0663, С3=0.209, С4=0.0698

Углы поворота кулачка, соответствующие подъему и опусканию коромысла, делим на восемь равных частей. Рассчитываем , и  при

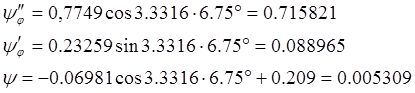
Для остальных углов поворота кулачка значения ,  и приведены в таблице 1. На рисунке 1 построены диаграммы движения коромысла.

№					R, мм			Rп,мм
0	0	0,7749	0	0	35,4877	46,28	0	25,48	0
1	6,75	0,71582	0,08896	0,304	35,8530	46,54	6,49	26,01	6,55
2	13,5	0,54759	0,16439	1,17	36,9015	47,22	12,56	27,55	12,67
3	20,25	0,29586	0,21483	2,46	38,4912	48,12	18,41	29,61	18,54
4	27	-0,0009	0,23259	3,99	40,3936	49,03	24,25	31,61	24,38
5	33,75	-0,2976	0,21497	5,52	42,3208	49,79	30,24	33,24	30,35
6	40,5	-0,5489	0,16466	6,82	43,9710	50,32	36,46	34,44	36,53
7	47,25	-0,7165	0,08931	7,69	45,0818	50,63	42,89	35,20	42,93
8	54	0	0	8	45,4752	50,73	49,54	35,47	49,54
9	59	0	0	8	45,4752	50,73	54,54	35,47	54,54
10	65,75	-0,7159	-0,0889	7,69	45,0850	50,63	61,39	35,17	61,36
11	72,5	-0,5481	-0,1644	6,82	43,9769	50,32	68,45	34,23	68,40
12	79,25	-0,2969	-0,2148	5,53	42,3284	49,79	75,74	32,73	75,66
13	86	-0,0006	-0,2325	4	40,4018	49,03	83,25	30,87	83,16
14	92,75	0,29581	-0,2149	2,47	38,4986	48,13	90,9	28,91	90,82
15	99,5	0,54726	-0,1646	1,17	36,9071	47,22	98,56	27,18	98,48
16	106,25	0,71549	-0,0893	0,306	35,8560	46,54	105,9	25,95	105,9
17	113	0,7748	0	0	35,4877	46,28	113	25,48	113

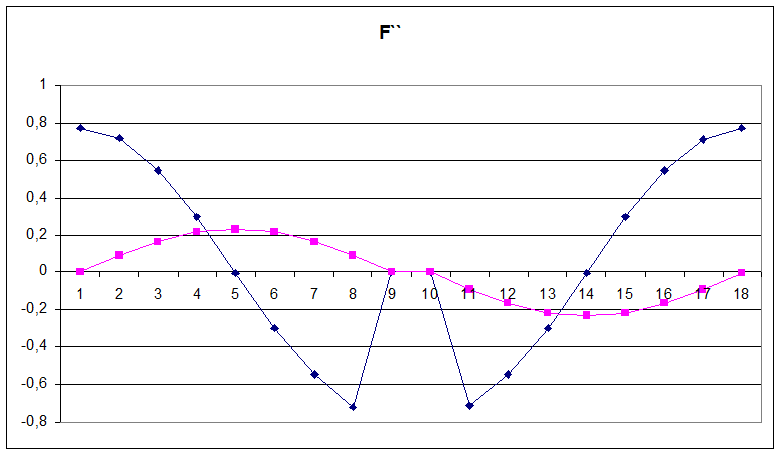
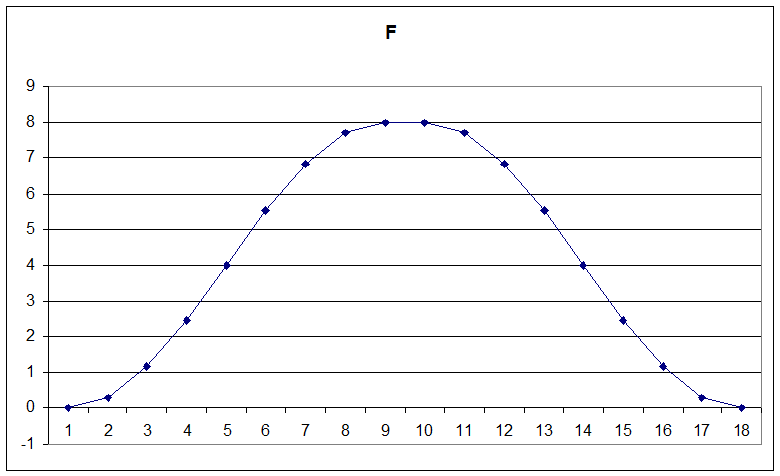
Рис. 1. Диаграмма движения коромысла

2. Для определения начального радиуса кулачка Ro необходимо найти lo – расстояние между центрами вращения кулачка и коромысла и  - угол между нижним положением коромысла и межосевой линией О1О2. Параметры и lo находим из условий ограничения угла давления () и получения минимальных размеров кулачкового механизма. Для случая вращения кулачка и коромысла на фазе подъема в противоположных направлениях:

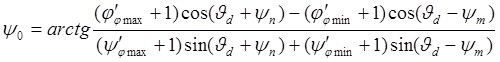                               (2.1)

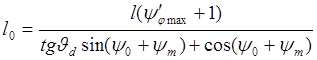,                                                            (2.2)

где - угол поворота коромысла на фазе подъема, при котором ; - угол поворота коромысла на фазе опускания, при котором

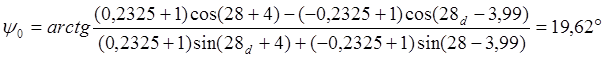
Принимаем .

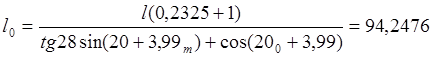мм                                                         Принимаем lo=95 мм.

3. Находим начальный радиус кулачка

4. Центровой профиль кулачка рассчитываем в полярных координатах по формулам:

                                                                       (4.1)

,                                                                                          (4.2)

где R – величина радиус-вектора центрового профиля кулачка;  - полярный угол;  и  - углы, определяемые из выражений:

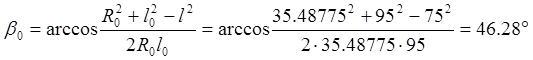
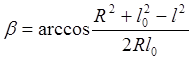                                                                                  (4.3)

В формуле (4.2) берется знак минус, если на фазе подъема направления вращения кулачка и коромысла противоположные, и знак плюс, если эти направления одинаковые.

При  будем иметь

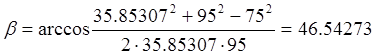
Для остальных углов поворота кулачка значения полярных координат и углов  приведены в таблице 1.

5. Для определения профиля кулачка выбираем радиус ролика из условий . Принимаем радиус ролика r=10мм. Величину радиуса – вектора и полярный угол профиля кулачка рассчитываем по формулам:

         (5.1)                                          (5.2)

В формуле (5.1)  - угол между радиусом – вектором центрового профиля и радиусом ролика

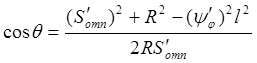                                                                       (5.3)

где

                                                                (5.4)

Здесь угол  при вращении кулачка и коромысла в противоположных направлениях и  при вращении в одном направлении. В выражении (5.2) - угол между радиусом – вектором центрового профиля и радиусом – вектора профиля кулачка.

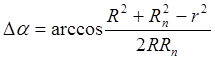                                                                                        (5.5)

Знак плюс в выражении (5.2) соответствует фазе подъема, а знак минус – фазе опускания коромысла.

Определяем полярные координаты профиля кулачка при .

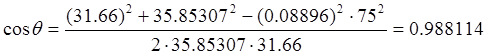
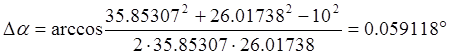
В остальных положениях механизма результаты расчетов приведены в таблице 1.

6. Строим центровой профиль и профиль кулачка.