2. Кинематический анализ рычажного механизма поперечно-строгального станка.
Кинематический анализ любого механизма состоит в определении: крайних (мертвых) положений станка; положений звеньев, включая и определение траекторий отдельных точек; скоростей и ускорений характерных точек звеньев по известному закону движения начального звена (обобщенной координаты).
Кинематический анализ механизмов проводят аналитическими и графическими методами. В курсовом проекте полученные результаты сравниваются между собой. Погрешность расчетов должна лежать в пределах 5…7%.
На первом этапе движения закон движения начального механизма не известен. Он определиться только после исследования динамики механизма. Поэтому при предварительном кинематическом анализе механизма вместо скоростей и ускорений исследуемых точек звеньев определяют их аналоги, которые не зависят от времени, а являются функциями обобщенной координаты. Для нахождения аналогов скоростей и ускорений необходимо определить крайние положения механизма и решить задачу о положениях отдельных точек звеньев.
2.1. Определение крайних (мертвых) положений механизма.
Крайние (мертвые) положения механизма можно находить аналитически и графически. Так как аналитика дает более высокую точность, то при определении крайних положений ей отдается предпочтение.
Крайние положения исследуемого механизма с вращательным движением начального звена определяются:
– видом первого простого механизма, присоединенного к начальному звену, если его выходное звено совершает возвратно-поступательное или возвратно-вращательное движение;
– видом второго простого механизма, присоединенного к вращающемуся выходному звену первого простого механизма, если выходное звено второго присоединенного механизма совершает возвратно-поступательное или возвратно-вращательное движение и так далее…
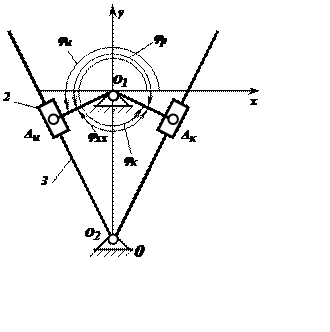
Для кулисного механизма с качающейся кулисой крайними являются такие положения, когда кривошип и кулиса взаимно перпендикулярны.
Расположим кулисный механизм так, чтобы одна из его координатных осей проходила по линии, соединяющей центры кинематических пар, которыми механизм присоединяется к стойкам, а вторая через стойку кривошипа. Тогда jр и jх будут углами рабочего и холостого хода механизма, а углы jн и jк – начальными и конечными углами, соответственно. Теперь, решая треугольники DО1АнО2 и DО1АкО2, найдем искомые углы jн и jк.
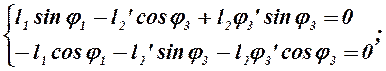
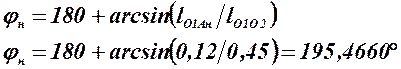
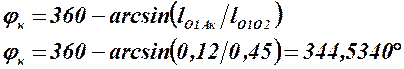
2.2. Определение положений звеньев механизма.
Положения звеньев механизма можно найти с помощью графических построений или аналитически.
2.2.1. Алгоритм построения планов положения исследуемого механизма.
Изображение кинематической схемы механизма, соответствующее определенному положению начального звена или начальных звеньев для механизмов с несколькими степенями свободы, называется планом механизма.
Построение планов положения проводим следующим образом.
1. Выбираем место расположения стойки начального звена и, соблюдая принятые обозначения, вычерчиваем ее.
2. Произвольно выбираем чертежный размер начального звена. Раствором циркуля, равным выбранному размеру, проводим тонкой линией траекторию движения начального звена (кривошипа).
3. Определяем
масштабный коэффициент длин 
[м/мм], где lK – истинная длина
кривошипа, lО1А – выбранный выше размер
чертежный размер кривошипа.
4. В
соответствии с формулой 
, находим чертежные и
координатные размеры всех остальных размеров механизма, где lBC – чертежная длина звена,
например, ВС; lЗ – истинный размер звена.
5. Наносим на чертеж все кинематические пары, которыми механизм присоединяется к стойке.
6. Тонкими линиями наносим все остальные известные заданные траектории движения звеньев и отдельных точек.
7. Откладываем на траекторию движения начального звена углы начального и конечного положения кривошипа. Тонкой линией изображаем кривошип в этих положениях.
8. Начиная от начального положения, разбиваем траекторию движения обобщенной координаты на двенадцать равных участков. Тонкой линией прорисовываем кривошип и его кинематические пары во всех этих положениях.
9. С помощью циркуля-измерителя, начиная от кривошипа, который находится в начальном положении, используя метод засечек, последовательно откладываем чертежные размеры звеньев механизма с учетом их траектории движения. Тонкими линиями прорисовываем звенья и кинематические пары. В результате получен план положения механизма в начальном положении.
10. Аналогично строим план для других положений механизма. Одно наиболее полно исследуемое положение механизма на плане положения изображаем толстой линией.
11. Строим траектории промежуточных точек звеньев. Для этого находим и отмечаем на звеньях во всех положениях искомые точки, а затем соединяем их в порядке последовательности плавной кривой. Полученные кривые и будут искомыми траекториями точек.
2.2.2. Построение планов положений исследуемого механизма.
Выбираем масштабный коэффициент длин и рассчитываем чертежные размеры звеньев. Так как для изображения плана положений используется среда AutoCAD 14.0, где предусмотрено масштабирование, звенья механизма изображаем в натуральную величину.
План механизма строим следующим образом:
– отмечаем на чертеже неподвижные точки О1 и О2, рисуем в них вращательные кинематические пары;
– на расстоянии Y от точки О1 проводим траекторию движения ползуна 5;
– проводим окружность радиусом О1А, которая является траекторией движения точки А и дугу с радиусом О2С, по которой движется точка С;
– на траектории движения точки А отмечаем крайние положения А1, А8, которые соответствуют крайним положениям исследуемого механизма;
– начиная от точки А1 – начала рабочего хода ползуна, окружность радиуса О1А делим на 12 равных частей;
– точки деления обозначаем А2, А3, А4 и так далее в направлении вращения кривошипа;
– строим положения кривошипа, соединяя точки Аj с точкой O1;
– методом засечек строим план положений механизма для каждого положения кривошипа;
– при построении планов механизма отмечаем положения центров масс звеньев 1, 3, 4 и строим их траектории;
– проставляем линейные и угловые размеры на чертеже в AutoCAD, и результаты измерений заносим в таблицу;
– определяем начальное D1 и конечное D8 положение точки D;
– строим над траекторией движения ползуна 5 график действия силы резания.
2.3. Кинематическое исследование машин и механизмов аналитическим методом.
Существует большое количество аналитических методов исследования кинематики машин и механизмов. Сущность всех этих методов заключается в том, что линейные и угловые координаты, скорости и ускорения точек звеньев механизма определяются в виде аналитических выражений. Аналитические выражения могут определять функцию явно, неявно или параметрически.
Исходными данными для вывода выражений является: структурная схема механизма, изображающая механизм в любом положении, исключая крайние; размеры звеньев; заданные положения обобщенных координат механизма; законы движения обобщенных координат механизма во времени. Если последнее не задано, то уравнения записываются в функции обобщенных координат, т.е. определяют не сами искомые функции, а их аналоги.
Рассмотрим применение метода замкнутых векторных контуров для определения линейных и угловых координат, скоростей и ускорений точек звеньев механизма.
Для определения кинематических характеристик механизма в соответствии с методом замкнутых векторных контуров поступаем следующим образом.
1. Рисуем в любом промежуточном положении структурную схему исследуемого механизма.
2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.
3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
