Для шарнирного кривошипно-коромыслового механизма крайними будут такие положения, когда кривошип и шатун то вытягиваются, то складываются в одну линию. Тогда φн и φк будут начальным и конечным углами механизма.
 |
Выбираем масштабный коэффициент длин ml = 0,003 м/мм и рассчитываем чертежные размеры звеньев.
Чертежные размеры звеньев
|
O1A, мм |
O2B мм |
BC,мм |
X , мм |
Y, мм |
|
50 |
74 |
200 |
24 |
24 |
Будем находить кинематические характеристики методом Зиновьева (метод замкнутых векторных контуров).
Структурную схему механизма располагаем в прямоугольной системе координат. Составляем векторные контуры.

Записываем уравнение замкнутости контура О1АO2 в векторном виде:
![]()
![]()
Этому уравнению соответствуют два уравнения проекций на оси координат:
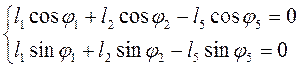
![]()
Записываем уравнение замкнутости контура O2BC в векторном виде:
![]()
Также проецируем данные вектора на оси координат:
Данные системы решаем с помощью программы MathCad (положение 1):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение первой системы дает по два значения, из которых необходимо выбрать соответствующие схеме механизма.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для нахождения положений точек S4 и S5 записываем следующие системы уравнений:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для положения 4 расчет ведется аналогично.
Все вычисленные величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в таблице:
Результаты расчета положений звеньев
(положение 1)
|
Величина |
j2,о |
j4,о |
L2 , мм |
L6 , ММ |
|
Графически |
161 |
-6 |
76 |
130 |
|
Аналитически |
161.5 |
-6.3 |
77 |
129 |
|
Отклонение, D %
|
0.3 |
4 |
1.2 |
0.7 |
(положение 4)
|
Величина |
j2,о |
j3,о |
l5 , мм |
L6 , ММ |
|
Графически |
131 |
16 |
36 |
145 |
|
Аналитически |
-130.5 |
15.96 |
35.3 |
144 |
|
Отклонение, D %
|
0.3 |
0.2 |
1.9 |
0.6 |
Найдём аналоги скоростей и ускорений.
Так как аналоги скоростей и ускорений
не зависят от закона изменения обобщенной координаты, принимаем ![]()
Дифференцируем по обобщенной координате систему уравнений для первого контура и решаем ее в MathCad:
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично поступаем и с системой уравнений для второго контура:
|
|
|
|
|
|
|
|
|
|
|
|
Аналоги скоростей центров масс звеньев 4 и 5 получаем в проекциях на оси координат, дифференцируя уравнения по обобщенной координате:
|
|
|
|
|
|
|
|
|
|
|
|
Расчеты приведены для положения 1, аналогично рассчитывается положение 4.
Аналитическое определение аналогов ускорений основано на повторном дифференцировании уравнений по обобщенной координате.
После дифференцирования уравнений получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналоги ускорений центров масс звеньев 4 и 5 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения.
|
|
|
|
|
|
|
|
|
|
|
|
Расчеты приведены для положения 1, аналогично рассчитывается положение 4.
Результаты расчетов аналогов скоростей и ускорений аналитическим и графическим методами сведем в таблицы
Результаты расчета аналогов скоростей
(положение 1)
|
Величина |
j’2 |
j’4 |
L2’ |
L6’ |
S4x’ |
S4y’ |
S5x’ |
|
Графически |
-35 |
-12 |
14 |
9 |
- |
- |
- |
|
Аналитически |
-35.28 |
-12.43 |
15 |
9 |
11.33 |
65 |
9 |
|
Отклонение, D %
|
0.7 |
3.4 |
4.1 |
0 |
- |
- |
- |
(положение 4)
|
Величина |
j’2 |
j’4 |
L2’ |
L6’ |
S4x’ |
S4y’ |
S5x’ |
|
Графически |
-60 |
-15 |
32 |
-45 |
- |
- |
- |
|
Аналитически |
-60.53 |
-15.22 |
33 |
-44 |
-51.3 |
77 |
-44 |
|
Отклонение, D %
|
0.8 |
1.4 |
3 |
2.2 |
- |
- |
- |
:
Результаты расчета аналогов ускорений
(положение 1)
|
Величина |
j’’2 |
j’’4 |
L2’’ |
L6’’ |
S4x’’ |
S4y’’ |
S5x’’ |
|
Графически |
70 |
20 |
-30 |
-2 |
- |
- |
- |
|
Аналитически |
70.56 |
20.86 |
-29.3 |
-2.07 |
-1.38 |
-58 |
-2.07 |
|
Отклонение, D %
|
0.7 |
4 |
2.3 |
3.3 |
- |
- |
- |
(положение 4)
|
Величина |
j’’2 |
j’’4 |
L2’’ |
L6’’ |
S4x’’ |
S4y’’ |
S5x’’ |
|
Графически |
122 |
28 |
-41 |
131 |
- |
- |
- |
|
Аналитически |
121.07 |
28.33 |
-40 |
130.67 |
151 |
5.33 |
130.67 |
|
Отклонение, D %
|
0.7 |
1.1 |
2.5 |
0.2 |
- |
- |
- |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.