Кинематический анализ рычажного механизма поперечно-строгального станка, страница 4

Величина	j3’°	l2’, м	j4’°	l8’, м	S3X’, м	S3Y’, м	S4X’, м	S4Y’, м	S5X’, м	S5Y’, м
Графически	0,1159	0,1054	0,0778	0,0925	–	–	–	–	–	–
Аналитически	-0,1159	0,1054	0,0778	-0,0925	0,0468	0,0113	0,0930	0,0113	0,0925	0,0
Отклонение, D %	0	0	0	0	0	0	0	0	0	0

2.4.2. Определение аналогов ускорений исследуемого станка графическим методом.

Задачу решаем путем построения плана ускорений, считая w₁ постоянной величиной:

1) Определяем ускорение точки А. Полное ускорение точки А равно нормальной составляющей , которая направлена по линии О₁А к центру А

, так как .

.

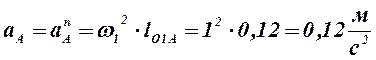2) Из точки p полюса плана ускорений – откладываем вектор, изображающий ускорение точки А, в виде отрезка pа = 12 мм.

3) Подсчитываем масштабный коэффициент ускорений:

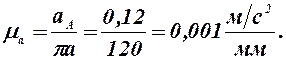
4) Для определения ускорения точки В, которая принадлежит одновременно и второму, и третьему звеньям, распишем векторное уравнение, определяющее ускорение для точки В, в составе второго звена:

Выразим отсюда ускорение точки В, принадлежащей третьему звену:

                                                                                      (2.34)

где      – абсолютное ускорение точки А, ;

 – ускорение, ;

 – кариолисово ускорение, его направление определяется поворотом относительно скорости  на 90° по направлению скорости w₃.

Величина вектора  определяется следующим образом:

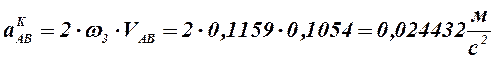                                    (2.35)

5) Запишем уравнение для определения ускорения точки В, как точки принадлежащей третьему звену:

,                                                                                                (2.36)

где      – нормальная составляющая вектора ускорения точки В, ;

           – касательная составляющая вектора ускорения точки В, ;

Величина вектора  определяется следующим образом:

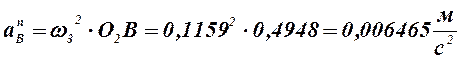.                                        (2.37)

Отрезки, изображающие в миллиметрах на плане ускорений векторы кариолисова (см. (2.35)) и нормального (см. (2.37)) ускорения, равны:

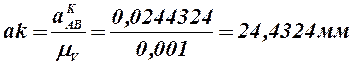
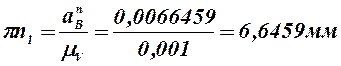
6) Так как в уравнениях (2.34) и (2.36) левые части равны (), то можем приравнять правые, и, затем, решая полученное выражение графически, найдем величину и направление вектора ускорения .

                                                                               (2.38)

Используя уравнение (2.34) из точки а откладываем отрезок аk, перпендикулярный скорости  в направлении w₃, который является обозначением , а затем через точку k проводим прямую по направлению , то есть параллельно О₂B.

Из полюса плана ускорений p, согласно уравнению (2.36), откладываем отрезок pп₁, параллельный O₂B. Это будет вектор . Далее перпендикулярно ему, то есть по направлению , проводим прямую.

Точка пересечения двух проведенных прямых, согласно уравнению (2.38), будет являться искомой точкой b – концом вектора ускорения точки В на плане ускорений.

7) Для определения ускорения точки С используем теорему подобия:

,

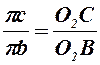откуда

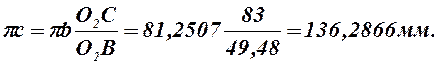
Отрезок pс откладываем на продолжении отрезка pb.

8) Ускорение точки d, которая является общей для звеньев 4 и 5, находим из уравнения

,        где     ;  ;    ;             (2.39)

Найдем величину вектора

,

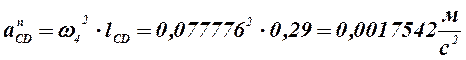откуда

.

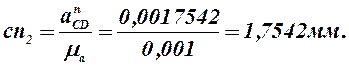Откладываем отрезок сn₂, изображающий в миллиметрах вектор ускорения , из точки С по линии параллельной к CD. Далее, следуя уравнению (2.39), проводим из точки п₂ линию, перпендикулярную к СD, а через полюс плана ускорений p проводим линию, параллельную оси х – х. Точка пересечения  этих линий есть точка d – конец вектора ускорения  точки D.

9) Ускорения точек S₁, S₃ и S₄ находим, используя теорему подобия:

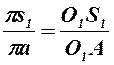, откуда

.

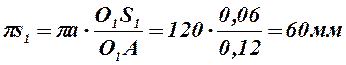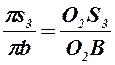, откуда

.

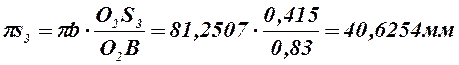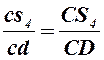, откуда

.

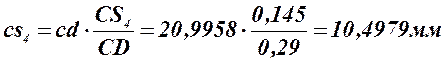10) Из плана ускорений находим:

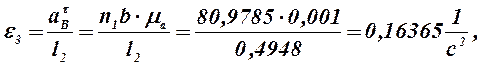
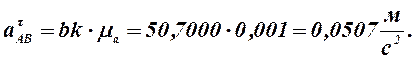
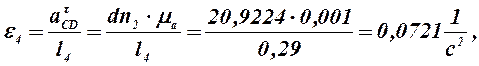
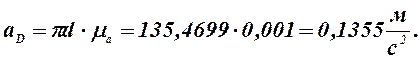
Так как при построении плана ускорений звеньев мы приняли w₁ = const, то

                                  

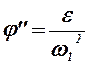
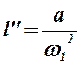
Учитывая, что 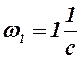, находим

                 

                 

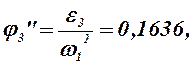
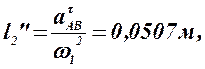
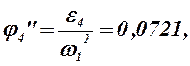
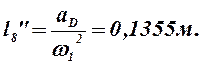
В табл. 2.3 приведены значения аналогов ускорений, полученные графическим и аналитическим методами.

Таблица 2.3.

Результаты расчета аналогов ускорений.

Величина	j3”°	l2”, м	j4”°	l8”, м	S3X”, м	S3Y”, м	S4X”, м	S4Y”, м	S5X”, м	S5Y”, м
Графически	0,1636	0,0507	0,0721	0,1355	–	–	–	–	–	–
Аналитически	-0,1636	-0,0507	0,0721	0,1355	0,0660	0,0105	0,1243	0,0726	0,1355	0,0000
Отклонение, D %	0	0	0	0	0	0	0	0	0	0

Величина отклонения D очень мала, так как результаты графического (с построением планов положений, скоростей и ускорений в AutoCAD) и аналитического методов отличаются в пределе 0,01%.

Аналогично проводим расчет кинематических параметров в остальных положениях механизма.