Кинематический анализ рычажного механизма поперечно-строгального станка, страница 2

4.  Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры (одни и те же векторы могут входить в разные контуры). Причем в каждый контур должно входить не более двух неизвестных величин. Разбивку контуров начинаем от звена, связанного с обобщенной координатой.

5.  Составляем векторные уравнения замкнутости полученных контуров. Если направление вектора совпадает с выбранным направлением обхода контура, то он в уравнение записывается со знаком плюс, в противном случае со знаком – минус.

6.  Спроектировав векторные уравнения замкнутости контуров на оси X и Y, получим базовые системы уравнений для определения кинематических характеристик звеньев и их отдельных точек.

Применим метод замкнутых контуров для исследуемого механизма.

Структурную схему механизма располагаем в прямоугольной системе координат, начало которой помещаем в точку О₁. Со звеньями механизма связываем векторы так, чтобы их последовательность образовывала два замкнутых контура О₁АО₂О₁ и О₂СDKО₂. При образовании контура учитываем, что в него должно входить не более двух неизвестных.

Записываем уравнение замкнутости первого контура О₁АО₂О₁ в векторной форме. Для этого обходим его периметр в направлении вектора `l₁, причем все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие – со знаком «–»:

                                                                                                 (2.1)

Уравнению (2.1) соответствуют два уравнения проекций на оси координат:

.

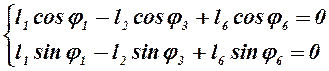Учитывая, что j₆ = 90°, преобразуем систему уравнений к следующему виду:

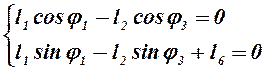.                                                                           (2.2)

Среди величин, входящих в уравнение (2.2), переменными являются углы j₁, j₃ и модуль вектора `l₂. Угол j₁ является обобщенной координатой механизма, и поэтому он должен быть задан. Из уравнений (2.2) подлежат определению переменные параметры j₃ и l₂.

Следовательно, из уравнений (2.2) находим угол наклона вектора `l₂:

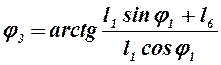;                                                                                  (2.3)

и его модуль:

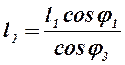.                                                                                                  (2.4)

Уравнение замкнутости второго контура О₂СDKО₂ имеет вид:

                                                                                                    (2.5)

или в проекции на оси координат:

.

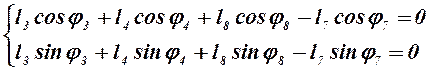Учитывая, что j₈ = 0° и j₇ = 90°, получим:

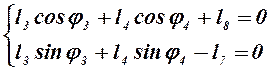.                                                                 (2.6)

Из уравнений (2.6) находим угол наклона вектора `l<sub>4</sub> – j<sub>4</sub> и модуль вектора `l₈:

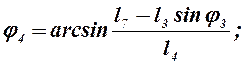                                                                               (2.7)

                                                                                (2.8)

Для определения положений точек S₃ и S₄ записываем уравнения замкнутости контуров О₁S₃O₂O₁ и O₁ACS₄O₁, соответственно.

                                                                                       (2.9)

                                                                        (2.10)

Из уравнений (2.9) и (2.10) находим координаты центров масс звеньев 3 и 4:

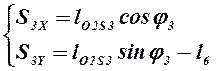,                                                                                 (2.11)

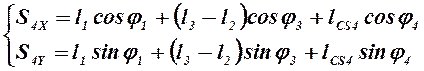,                                              (2.12)

где

Для нахождения координат центра масс 5 звена рассмотрим исследуемый механизм в начальном положении, т.е. при j₁ = 195,4660°.

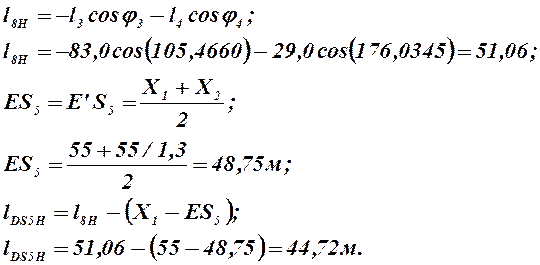
Тогда координаты центра масс 5 звена определятся следующим образом:

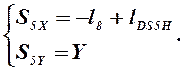                                                                                       (2.13)

С целью проверки правильности полученных выражений производим расчет по формулам (2.3), (2.4), (2.7), (2.8), (2.11), (2.12) и (2.13) при значении обобщенной координаты соответствующей второму положению начального звена.

Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в табл. 2.1.

Таблица 2.1.

Результаты расчета положений звеньев.

Величина	j1°	j3°	l2, м	j4°	l8, м	S3X, м	S3Y, м	S4X, м	S4Y, м	S5X, м	S5Y, м
Графически	165	103,5472	0,4948	177,4123	0,4841	-0,0972	-0,0465	-0,3393	0,3635	-0,037	0,3700
Аналитически	165	103,5472	0,4948	177,4123	0,4841	-0,0972	-0,0465	-0,3393	0,3635	-0,037	0,3700
Отклонение, D %,	0	0	0	0	0	0	0	0	0	0	0

Определение кинематических свойств механизма, когда закон движения начального звена еще не известен, производится с помощью кинематических характеристик, называемых аналогами скоростей и ускорений, которые не зависят от времени, а являются функциями обобщенной координаты.

Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (2.2) и (2.6). Продифференцировав уравнения (2.2), соблюдая условие, что вектор `l₆ – не зависит от обобщенной координаты, получим