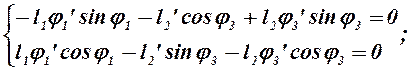 (2.14)
(2.14)
где j1’ – аналог угловой скорости звена 1. В расчетах принимаем ![]() ,
так как угловая скорость звена 1
направлена по ходу часовой стрелки; j3’ – аналог угловой скорости звена 3, l2’ – аналог переносной (поступательной) скорости точки В.
,
так как угловая скорость звена 1
направлена по ходу часовой стрелки; j3’ – аналог угловой скорости звена 3, l2’ – аналог переносной (поступательной) скорости точки В.
При дифференцировании уравнений (2.6) учитываем, что вектор `l7 – не зависит от обобщенной координаты, в итоге получаем
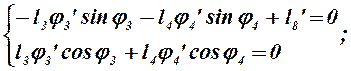 (2.15)
(2.15)
где j4’ – аналог угловой скорости звена 4, l8’ – аналог скорости точки D.
Решая (2.14) и проведя следующие преобразования:
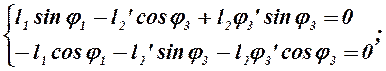
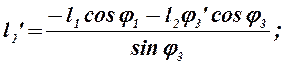
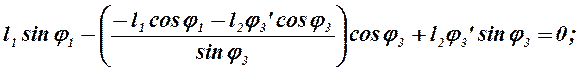
![]()
![]()
![]()
находим соответственно j3’:
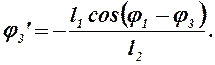 (2.16)
(2.16)
и l2’:
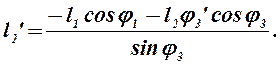 (2.17)
(2.17)
Из уравнений (2.15) соответственно находим:
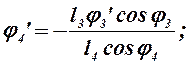 (2.18)
(2.18)
![]() (2.19)
(2.19)
Аналоги скоростей центров масс звеньев 3, 4 и 5 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.11), (2.12) и (2.13):
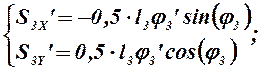 (2.20)
(2.20)
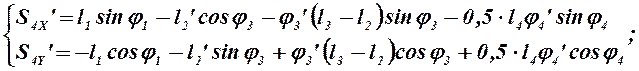 (2.21)
(2.21)
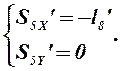 (2.22)
(2.22)
Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.14) и (2.15):
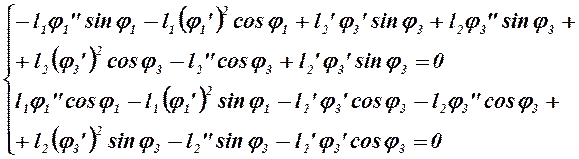 (2.23)
(2.23)
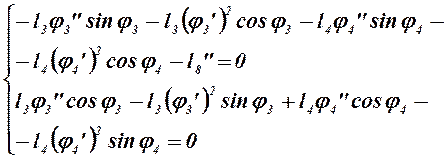 (2.24)
(2.24)
Второе уравнение системы (2.23) имеет вид:
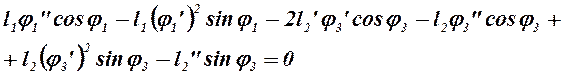
Вычтем из аргументов всех тригонометрических функций указанного выше уравнения угол j3:
![]()
и выразим j3”:
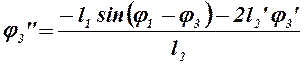 .
(2.25)
.
(2.25)
Из аргументов всех тригонометрических функций первого уравнения вычтем угол j3, имеем:
![]()
![]() (2.26)
(2.26)
Из уравнений (2.24) находим значения j4” и l8 соответственно:
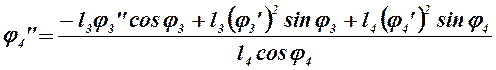 (2.27)
(2.27)
![]() .
(2.28)
.
(2.28)
Дифференцируя по обобщенной координате уравнения (2.20), (2.21) и (2.23), определяем аналоги ускорений центров масс звеньев 3, 4 и 5 в проекциях на оси координат:
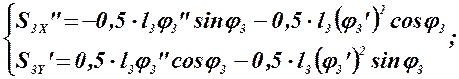 (2.29)
(2.29)
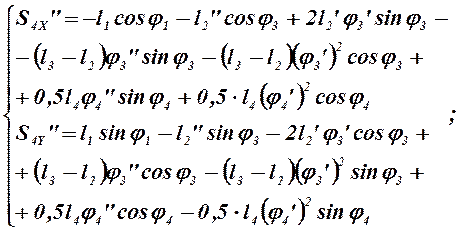 (2.30)
(2.30)
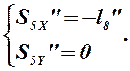 (2.31)
(2.31)
По полученным формулам находим аналоги скоростей и ускорений интересующих точек и звеньев.
2.4. Построение планов скоростей и ускорений.
Планом скоростей (ускорений) называют рисунок, на котором в масштабе изображены векторы, равные по модулю и направлению скоростям (ускорениям) различных точек звеньев механизма в данный момент времени.
План скоростей (ускорений) механизма, построенный для исследуемого положения механизма, является совокупностью нескольких планов скоростей (ускорений) отдельных точек звеньев, у которых полюса планов являются общей точкой – полюсом плана скоростей (ускорений) механизма.
2.4.1. Определение аналогов скоростей исследуемого станка графическим методом
Решение этой задачи графическим методом основано
на построении плана скоростей для второго положения механизма при ![]() . Так как аналоги скоростей и ускорений не зависят от закона
изменения обобщенной координаты, принимаем w1 = 1 рад/с.
. Так как аналоги скоростей и ускорений не зависят от закона
изменения обобщенной координаты, принимаем w1 = 1 рад/с.
План скоростей строим в следующем порядке:
1) находим скорость точки А:
![]() ;
(2.32)
;
(2.32)
2) из полюса плана скоростей рV – откладываем отрезок рVа = 12мм, изображающий вектор скорости точки А;
3) подсчитываем масштабный коэффициент плана скоростей:
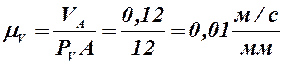 ;
;
4) для определения скорости точки В раскладываем плоскопараллельное движение звена 3 на переносное (поступательное) вместе с точкой А и относительное (вращательное) вокруг точки А. Поэтому
![]() , где
, где ![]() ,
, ![]() и
и ![]() (2.33)
(2.33)
Уравнение
(2.33) решаем графически. Через точку а проводим линию, параллельную О2В, а через полюс рV – линию, перпендикулярную
О2В, до их пересечения в
точке b. Векторы рVb и аb изображают искомые
скорости ![]() и
и ![]() ;
;
5) скорость точки С звена 3 определяем, используя теорему подобия
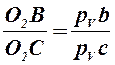 ,
,
откуда
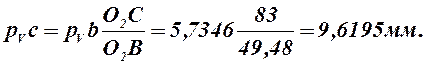
Отрезок pVс откладываем от полюса pV на продолжении отрезка pVb;
6) скорость точки d, которая является общей для звеньев 4 и 5, находим раскладывая движение точки D на переносное (вращательное) вместе с точкой С и относительное (поступательное) по отношению к точке С. В абсолютном движении точка D перемещается вдоль оси х–х. Поэтому
![]() , где
, где ![]() ,
, ![]() и
и ![]() .
.
Через точку с проводим линию перпендикулярную CD, а через полюс pV – линию, параллельную х–х, до пересечения их в точке с. Вектор pVс; изображает скорость точки с;
7) положения точек S3 и S4 на плане скоростей находим, воспользовавшись теоремой подобия:
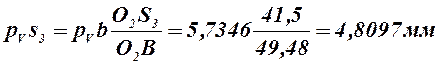
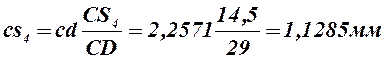
Векторы pVs3 и pVs4 изображают скорости ![]() и
и ![]() . Скорость точки S5 равна скорости точки D;
. Скорость точки S5 равна скорости точки D;
8) из плана скоростей находим:
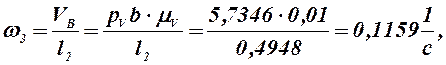
![]()
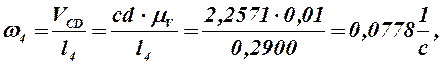
![]()
Определяем аналоги линейных и угловых скоростей:
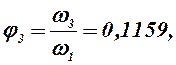
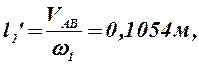
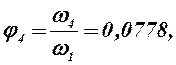
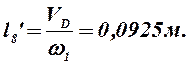
В табл. 2.2 приведены значения аналогов скоростей, полученные графическим и аналитическими методами:
Таблица 2.2.
Результаты расчета аналогов скоростей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.