Кинематический анализ рычажного механизма, страница 2

                    

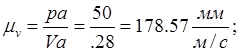
4). для определения скорости точки В раскладываем плоскопараллельное движение звена 2 на переносное (поступательное) вместе с точкой А и относительное (вращательное) вокруг точки А. Так как точка В совершает только поступательное движение параллельно оси 0x, то:

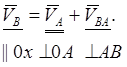                                                                                                                                 (2.19)

Уравнение (2.19) решаем графически. Через тоску А проводим линию, перпендикулярную АВ, через полюс p – линию, параллельную 0x, до их пересечения в точке b. Векторы и изображают искомые скорости  и ;

5). скорость точки D звена 2 определяем, раскладывая плоскопараллельное движение звена 2 на переносное вместе с точкой А и относительное вокруг точки А. И с другой стороны , раскладывая плоскопараллельное движение звена 2 на переносное вместе с точкой B и относительное вокруг точки B. Поэтому:

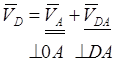                                                                                                                                  (2.20)

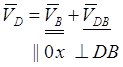                                                                                                                                 (2.21)

Уравнения (2.20) и (2.21) решаем графически. Через точку А проводим линию, перпендикулярную АD, а через точку В проводим линию, перпендикулярную ВD, до их пересечения в точке d. Из полюса p проводим линию в точку d. Векторы  изображают искомые скорости .

6). скорость точки E звена 4 определяем, раскладывая плоскопараллельное движение звена 4 на переносное вместе с точкой D и относительное вокруг точки D. И с другой стороны , точка E находится в относительном движении вокруг неподвижной точки О₁. Поэтому:

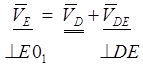                                                                                                                             (2.22)

Уравнение (2.22) решаем графически. Через тоску D проводим линию, перпендикулярную DE, через полюс p – линию, перпендикулярную EО₁, до их пересечения в точке e. Векторы и изображают искомые скорости  и ;

Скорость точки F направлена ^ звену O₁F. Величину находим из отношения:

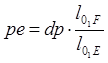
7). положения точек s₂ и s₄ на плане скоростей находим, воспользовавшись теоремой подобия:

                 

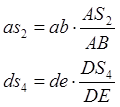
Векторы и  изображают скорости  и . Скорость точки S₃ равна скорости точки В. Скорость точки S₅равна 0.

8). из плана скоростей находим:

                  ; ;

                   

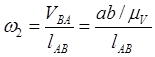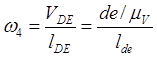
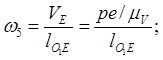
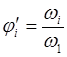
В табл. 2.3 приведены значения аналогов скоростей, полученные графическим и аналитическим способами.

Таблица 2.3

Величина	j’2	l’3, S’3, м	j’4	j’5	S2`x	S2`y	S4`x	S4`y
Графически	0,258	0,176	-0,115	0,734	0,151	-0,17	0,134	-0,079
Аналитически	0,258	0,176	-0,115	0,734	0,151	-0,17	0,134	-0,079
D %	0	0	0	0	0	0	0	0

Результаты расчета аналогов скоростей

2.4.2. Определение аналогов ускорений исследуемого механизма графическим методом

Задачу решаем путем построения плана ускорений, считая w₁ постоянной величиной.

1.  Находим ускорение точки А. Полное ускорение точки А равно нормальной составляющей , которая направлена по линии 0₁А к центру 0₁

2.  Из точки p - полюса плана ускорений – откладываем вектор, изображающий ускорение точки А, в виде отрезка pa = 96 мм;

3.  Подсчитываем масштабный коэффициент ускорений :

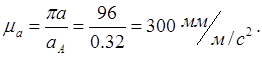
4.  Для определения ускорения точки B записываем векторное уравнение

 

Нормальные ускорения вычисляем по формулам:

               

Вектор  направлен вдоль линии АВ. Через точку n₁  плана ускорений проводим направления вектора касательного ускорения (перпендикулярное нормальному), пересечение с горизонталью определяет точку b.

 

5.  Для определения ускорения точки D записываем следующие векторные уравнения, рассматривая движение этой точки вначале со звеном  АD, а затем со звеном ВD:

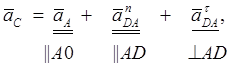
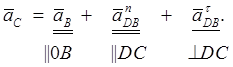
Нормальные ускорения вычисляем по формуле:

                     

                     

Вектор  направлен вдоль линии DА от точки D к точке A – центру относительного вращения звена, а вектор  - по линии DВ от точки D к центру B. Через точки n₂  и n₃ плана ускорений проводим направление векторов касательных ускорений (перпендикулярно нормальному), пересечение которых определяет точку d – конец вектора искомого ускорения точки D. Векторы ,  и  изображают искомые ускорения ,  и .

6.  Для определения ускорения точки E записываем следующие векторные уравнения, рассматривая движение этой точки вначале со звеном  2, а затем со звеном 4:

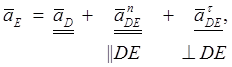
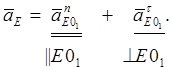
Нормальные ускорения вычисляем по формуле:

                     

                     

Вектор  направлен вдоль линии DE от точки E к точке D – центру относительного вращения звена, а вектор  - по линии 0₁E от точки E к центру 0₁. Через точки n₄  и n₅ плана ускорений проводим направление векторов касательных ускорений (перпендикулярно нормальному), пересечение которых определяет точку e – конец вектора искомого ускорения точки E. Векторы,  и  изображают искомые ускорения ,  и .

7.  Ускорения точек S₂ и S₄ определяем, используя теорему подобия. Положение точки s₂ находим из выражения:

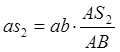
Точка s₄ на плане ускорений делит отрезок cd пополам.

                     

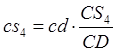
Ускорение точки S₃ равно ускорению точки В, а ускорение точки S₅ равно нулю.

В табл. 2.4 приведены значения аналогов ускорений, полученные графическим и аналитическим методами.

Таблица 2.4

Результаты расчета аналогов ускорений

Величина	j’’2	l’’3	j’’4, м	j’’5	s’’2X, м	s’’2Y, м	s’’4X, м	s’’4Y, м
Графически	0,139	0,286	-0,654	-0,793	-0,255	-0,098	-0,167	0,047
Аналитически	0,139	0,286	-0,654	-0,793	-0,255	-0,098	-0,167	0,047
D %	0	0	0	0	0	0	0	0