3.Кинематический анализ механизма долбёжного станка.
3.1. Определение крайних положений механизма.
Для кулисного механизма с качающейся
кулисой крайними являются положения, в которых кулиса и кривошип взаимно
перпендикулярны. Расположим механизм так, чтобы одна из его координатных осей
проходила по линии, соединяющей центры кинематических пар, которыми механизм
присоединён к стойкам, а вторая через стойку кривошипа. Тогда ![]() и
и ![]() будут
углами рабочего и холостого хода механизма, а углы
будут
углами рабочего и холостого хода механизма, а углы ![]() и
и
![]() начальными и конечными углами
соответственно (рис.3.1).
начальными и конечными углами
соответственно (рис.3.1).
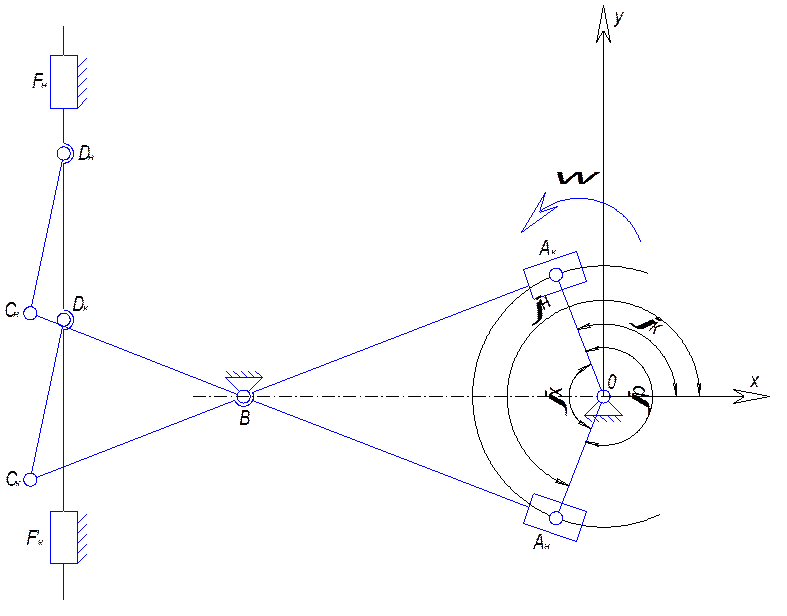
Рис.3.1. Определение крайних положений механизма
Решая
треугольник ![]() , найдём искомые углы
, найдём искомые углы ![]() :
:
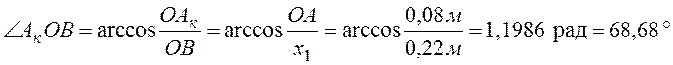 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
3.2. Определение положений звеньев и точек механизма.
3.2.1. Кинематическое исследование механизма графическим способом.
Выбираем
масштабный коэффициент длин  , где
, где ![]() -истинная длина кривошипа,
-истинная длина кривошипа, ![]() -выбранный чертёжный размер
кривошипа. Рассчитываем чертежные размеры звеньев (табл.3.1).
-выбранный чертёжный размер
кривошипа. Рассчитываем чертежные размеры звеньев (табл.3.1).
Чертёжные размеры звеньев
Таблица 3.1
|
OA,мм |
BC,мм |
CD,мм |
|
|
|
32 |
56 |
40 |
88 |
44 |
Планы механизма (рис.3.2) строим следующим образом:
-отмечаем на чертеже неподвижные точки О и В, рисуем в них вращательные кинематические пары;
-на расстоянии ![]() от
точки В проводим траекторию движения ползуна (5);
от
точки В проводим траекторию движения ползуна (5);
-проводим окружность радиусом ОА, которая является траекторией движения точки А, и дугу с радиусом ВС, по которой движется точка С.
-на траектории движения точки A отмечаем крайние положения ![]() ,
которые соответствуют крайним положениям исследуемого механизма;
,
которые соответствуют крайним положениям исследуемого механизма;
-начиная от точки ![]() -
начала рабочего хода кривошипа, делим окружность на 12 равных сегментов;
-
начала рабочего хода кривошипа, делим окружность на 12 равных сегментов;
-точки деления обозначаем через ![]() и т.д. в направлении рабочего хода;
и т.д. в направлении рабочего хода;
-строим положения коромысла, соединяя
точки ![]() c точками
c точками ![]() .
.
-при построении планов механизма отмечаем положения центров масс звеньев (3) и (4) и строим их траектории;
-проверяем с помощью линейки и транспортира углы наклона и длины звеньев, результаты измерений заносим в таблицу (табл.3.2);
-строим справа от траектории движения ползуна (5) график действия силы долбления.
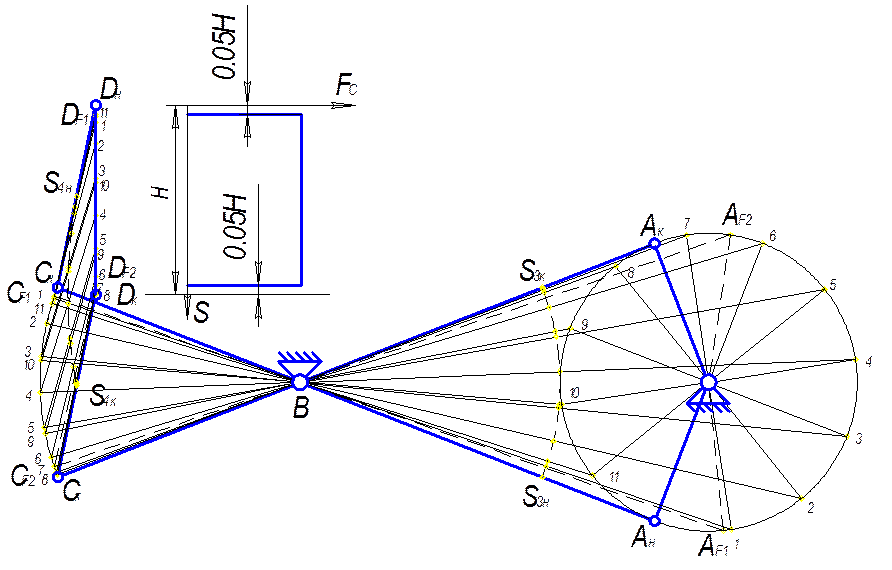 |
Рис.3.2. Планы механизма
3.2.2. Кинематическое исследование механизма аналитическим методом.
Для определения кинематических характеристик механизма применим метод замкнутых векторных контуров.
1. Рисуем во втором промежуточном положении структурную схему исследуемого механизма.
2. Выбираем координатную систему. Обычно начало координат связывают со стойкой начального звена.
3. В соответствии с методом все звенья механизма, включая и стойку, заменяют векторами произвольного направления. Положение в пространстве этих векторов характеризуется углами, величина которых определяется мысленным поворотом против хода часовой стрелки, помещенной в их начало, оси Х до направления соответствующего вектора.
4. Полученные векторы объединяем между собой так, чтобы они образовывали замкнутые контуры: OABO, BCDEB (рис.3.3).
Рис.3.3. Построение векторных контуров
В каждый контур должно входить не более двух неизвестных величин. Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора BC. Все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие - со знаком «–»:
![]() (3.1)
(3.1)
Уравнению (3.1) соответствуют два уравнения проекций на оси координат:
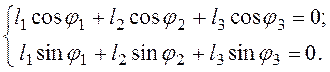 (3.2)
(3.2)
Среди величин, входящих в уравнения (3.2),
переменными являются углы ![]() и отрезок АВ.
Угол
и отрезок АВ.
Угол ![]() является обобщённой координатой
механизма, и поэтому он задан. Из уравнений (3.2) подлежат определению
переменные параметры
является обобщённой координатой
механизма, и поэтому он задан. Из уравнений (3.2) подлежат определению
переменные параметры ![]() . Перепишем уравнения
(3.2), учтя что
. Перепишем уравнения
(3.2), учтя что ![]() :
:
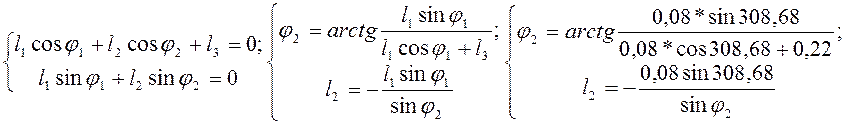
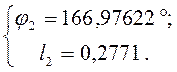
Проецируем контур BCDEB
на ось ОХ, учтём что ![]() :
:
![]() (3.3)
(3.3)
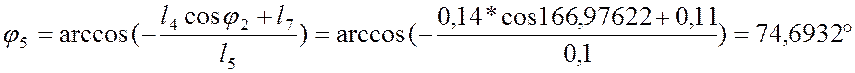
Проецируем этот контур на ось OY, учтем что ![]() :
:
![]()
Для нахождения
координат центров масс звеньев (2) и (3) записываем уравнения проекций векторов
![]() на оси:
на оси:
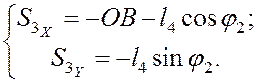 (3.4)
(3.4) 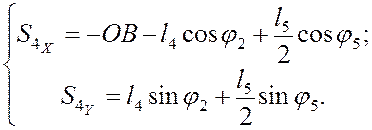 (3.5)
(3.5)
Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана механизма. Результаты сравнения приведены в таблице (табл.3.2).
Результаты расчёта положений звеньев
Табл.3.2.
|
Величина |
|
|
АВ, м |
|
DE,м |
|
Графически |
308,68 |
166,97622 |
0,2771 |
74,6932 |
0,12800237 |
|
Аналитически |
308,68 |
166,97622 |
0,2771 |
74,6932 |
0,128 |
|
Отклонение, |
0 |
0 |
0 |
0 |
0 |
3.3. Определение аналогов скоростей и скорений.
3.3.1. Определение аналогов скоростей аналитическим методом.
Так как аналоги скоростей и ускорений не
зависят от закона изменения обобщенной координаты, принимаем ![]() рад/с.
рад/с.
Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений (3.2) и (3.3). После дифференцирования уравнений (3.2) получим:
 где
где ![]() - аналог угловой скорости звена (1).
В расчетах примем
- аналог угловой скорости звена (1).
В расчетах примем ![]() - аналог угловой скорости
звена (2),
- аналог угловой скорости
звена (2), ![]() -аналог относительной скорости точки G. После упрощения имеем:
-аналог относительной скорости точки G. После упрощения имеем:
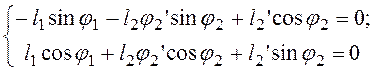 (3.6) Решая это
уравнение, имеем:
(3.6) Решая это
уравнение, имеем:
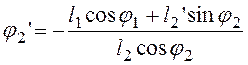 (3.7)
(3.7)
![]() (3.8)
(3.8)
Из уравнения
(3.3) соответственно находим ![]() :
:
![]() (3.9), откуда
(3.9), откуда
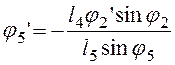 (3.10)
(3.10)
![]()
Аналоги скоростей центров масс звеньев (3) и (4) получаем в проекциях на оси координат, дифференцируя по обобщённой координате уравнений (3.4) и (3.5):
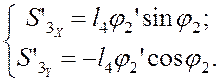 (3.11)
(3.11) 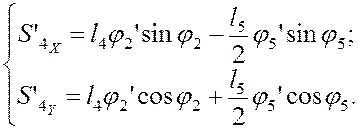 (3.12)
(3.12)
3.3.2. Определение аналогов ускорений аналитическим методом.
Аналитическое определение аналогов ускорений основано на дифференцировании по обобщённой координате уравнений (3.6), (3.9):
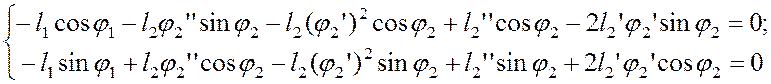 (3.13)
(3.13)
![]() (3.14)
(3.14)
В этих уравнениях ![]() -аналоги
угловых ускорений звеньев (2) и (5);
-аналоги
угловых ускорений звеньев (2) и (5); ![]() -аналог
относительного ускорения точки G. Для вычисления
-аналог
относительного ускорения точки G. Для вычисления ![]() решаем систему (3.13):
решаем систему (3.13):
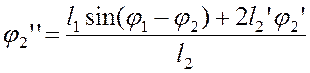 (3.15)
(3.15)
![]() (3.16)
(3.16)
Из уравнения (3.14):
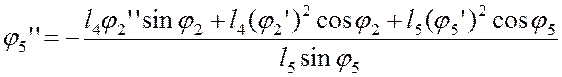 (3.17)
(3.17)
![]()
Дифференцируя по обобщённой координате уравнения (3.11) и (3.12), устанавливаем аналоги ускорений центров масс звеньев (3) и (4) в проекциях на оси координат:
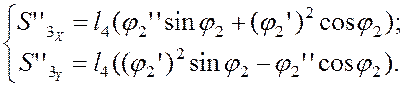 (3.18)
(3.18)
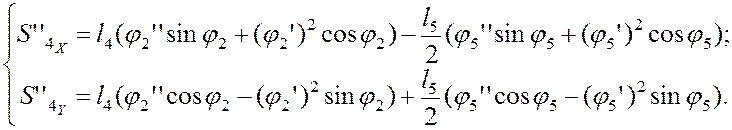 (3.19)
(3.19)
По полученным формулам находят аналоги скоростей и ускорений интересующих точек и звеньев. Результаты расчетов сводим в таблицы (Табл.3.3, 3.4, 3.5).
Результаты расчёта положений звеньев
Табл. 3.3.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.