Кинематический анализ механизма долбёжного станка, страница 5

3.3.3. Определение аналогов скоростей графическим методом.

 Определение аналогов скоростей графическим методом основано на построении плана скоростей для второго положения механизма при  (рис.3.4,а).Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем .

План скоростей механизма строим в следующем порядке:

1)  находим скорость точки А относительно точки О:

2)  из полюса плана скоростей p откладываем отрезок pa=50 мм, изображающий вектор скорости точки A (рис. 3.4,б);

3)  подсчитываем масштабный коэффициент скоростей: ;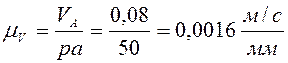

4)  точки звеньев (2) и (5), совпадающие в рассматриваемом положении с точками A и D, обозначим . Для группы ОА будем иметь следующую систему уравнений для определения скоростей звеньев группы:

,            

или

Так как , то

Через точку а проводим прямую в направлении скорости , параллельную  направлению звена (3), а через точку p – в направлении скорости , перпендикулярную к звену (3). Точка а2 пересечения двух проведенных прямых дает конец вектора скорости  точки , принадлежащей звену (1). Величина скорости

5) найдем угловую скорость звена (3):

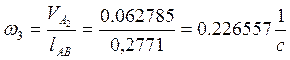
6) найдем скорость точки С:

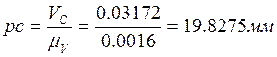
Вектор pc откладываем перпендикулярно звену (3) в направлении .

7) для группы СD имеем следующую систему уравнений для определения скоростей звеньев:

,          

или .

Так как , то

Через точку c проводим прямую в направлении скорости , перпендикулярную направлению звена (4), а через точку p – в направлении скорости , параллельную звену (5). Точка d пересечения двух проведенных прямых дает конец вектора скорости  точки D, принадлежащей звену (4). Величина скорости

Угловая скорость звена (4):

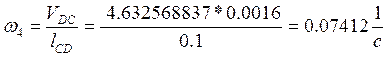
8) найдем скорость точки А1 относительно точки A из построений:

м/с

9) положения точек  на плане скоростей находим, воспользовавшись теоремой подобия:

,

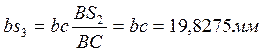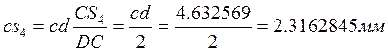
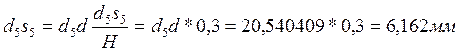
10) определяем аналоги линейных и угловых скоростей:

                              

                                            

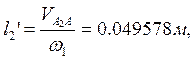
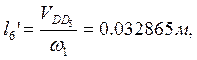
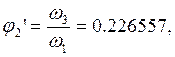
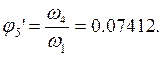
В таблице (табл. 3.6) приведены значения аналогов скоростей, полученные графическим и аналитическим методами.

Табл. 3.6.

Результаты расчетов аналогов скоростей

3.3.4. Определение аналогов ускорений графическим методом.

Задачу решаем путем построения плана ускорений, считая  постоянной величиной.

1) находим ускорение точки А. Так как , то . Полное ускорение точки А равно нормальной составляющей , которая направлена по линии ОА к центру О.

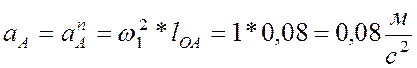
2) из точки π- полюса плана ускорений- откладываем вектор, изображающий ускорение точки А, в виде отрезка (рис. 3.4,в)

3) Подсчитываем масштабный коэффициент ускорений:

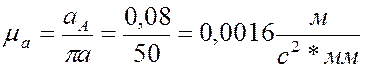
4)Ускорение точки , которая является общей для звеньев (2) и (3), находим из уравнений:

Учтем, что , -кориолисово ускорение, направление которого определяется поворотом относительной скорости  на 90° по направлению переносной угловой скорости  (рис.3.4,в). - относительное ускорение.

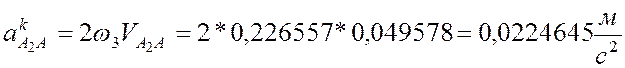
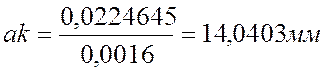
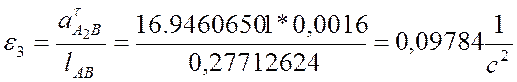
5) для расчета ускорения точки С звена (3) воспользуемся следующими формулой:

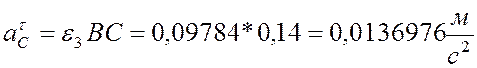
Проведем прямые в направлении нормального ускорения точки С и в направлении полного ускорения точки , пересечение прямых даст полное ускорение точки С.

6) для определения ускорений звеньев группы CD будем иметь систему уравнений:

Так как ось направляющей звена (5) неподвижна, то ускорение  равны 0. Тогда окончательное уравнение примет вид:

Через точку с проводим прямую параллельно отрезку СD. На ней откладываем вектор, равный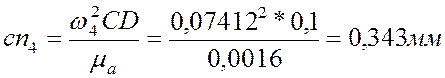

Через точку  проводим прямую, перпендикулярно звену CD, а через точку π – прямую параллельно оси Y. Пересечение двух этих прямых дает ускорение точки D.

7) Ускорения точек определяем, используя теорему подобия. Точка  лежит в центре вращения кривошипа (1), т.е. в точке О, поэтому её ускорение равно 0. , ускорение точки  численно равно ускорению точки С. Точка  делит отрезок CD пополам, поэтому ускорение точки  в 2 раза меньше ускорения точки D.  Ускорение точки  будет равно ускорению точки D и будет совпадать с ним на плане ускорений.

8) из плана ускорений получаем:

;

;

 .

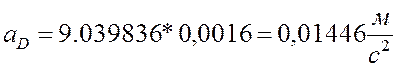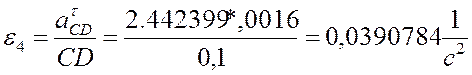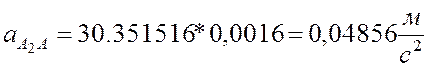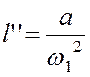Направления угловых скоростей и ускорений звеньев показаны на (рис.3.4,а). Так как при построении плана ускорений мы приняли , то:                                                 и        .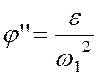

Учитывая, что 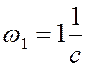, имеем:

                                        ,

,                                    

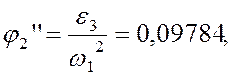
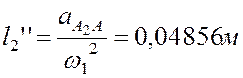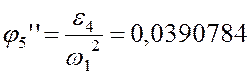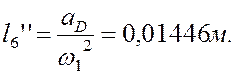
В таблице (табл.3.7) приведены значения аналогов ускорений, полученные графическим и аналитическим методами.

Табл.3.7.

Результаты расчета аналогов ускорений

Величина	φ''2	φ''5	L''2	L''6	S'' 3x	S'' 3y	S''4x	S''4y
Графически	0,09784	0,0390784	-0,04856	-0,01446	-	-	-	-
Аналитически	0,097838	0,039080872	-0,0485608	-0,01446	-0,00391	0,014964	-0,00587	-0,01471
∆%	0,002	0,0063	0,0016	0	-	-	-	-

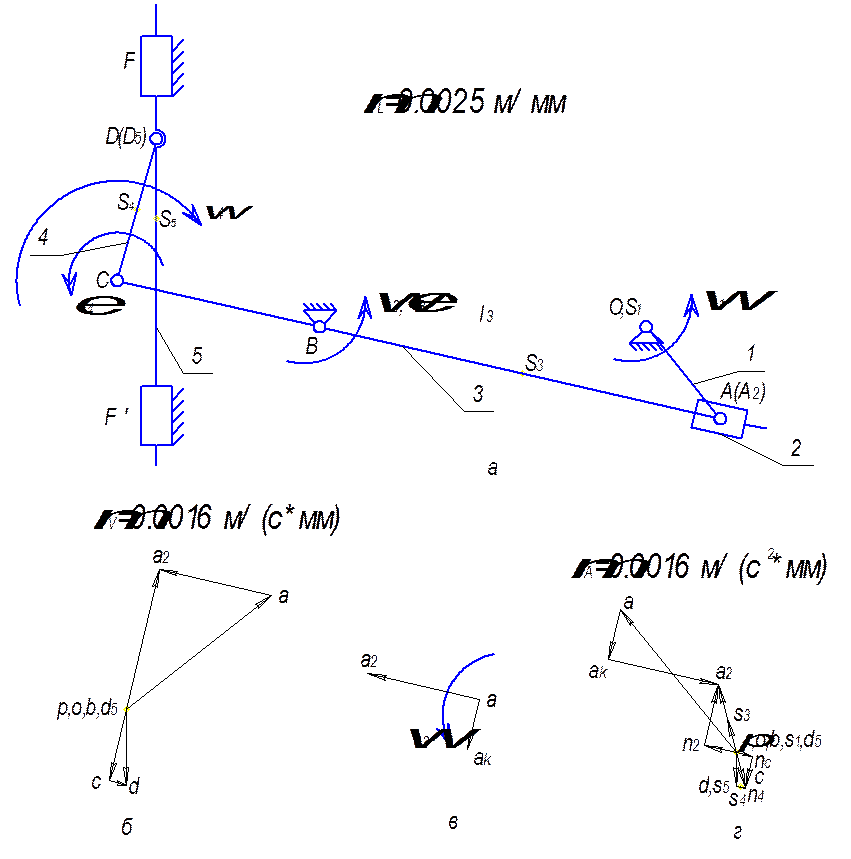 Рис.3.4. Планы скоростей и ускорений исследуемого механизма.