Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (3.12), (3.15)
Для первого контура:
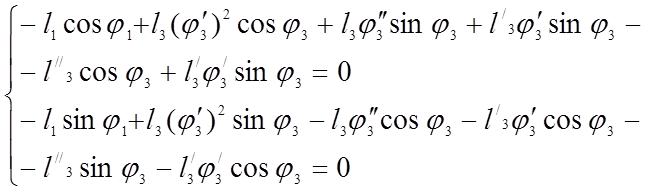 (3.20)
(3.20)
Решив (3.20) найдём ![]() и
и ![]() :
:
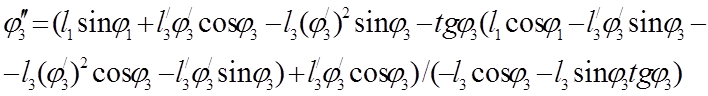 (3.21)
(3.21)
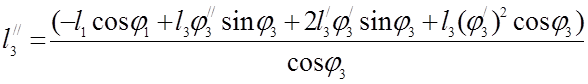 (3.22)
(3.22)
Для второго контура: :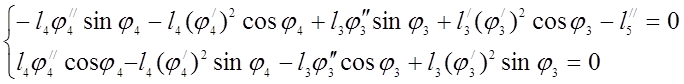 (3.23)
(3.23)
:Решив (3.23) найдём ![]() и
и ![]()
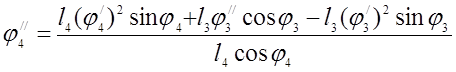 (3.24)
(3.24)
![]() (3.25)
(3.25)
Дифференцируя по обобщенной координате уравнения (3.18) и (3.19), устанавливаем аналоги ускорений центров масс звеньев 3 и 4 в проекциях на оси координат:
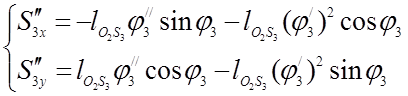 (3.26)
(3.26)
(3.27)
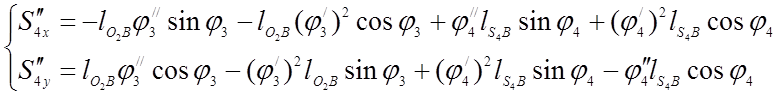 Т а б л и ц а (3.6)
Т а б л и ц а (3.6)
|
φ''3 |
l''3 |
φ''4 |
l''5 |
s''3x |
s''3y |
s''4x |
s''4y |
|
-0,1618 |
-3E-05 |
-0,0387 |
0,09441 |
-0,025 |
-0,0041 |
-0,1123 |
-0,0129 |
|
-0,1466 |
-0,0014 |
-0,0728 |
0,08769 |
-0,0226 |
-0,0077 |
-0,1024 |
-0,0236 |
|
-0,1296 |
-0,0026 |
-0,1009 |
0,08188 |
-0,0201 |
-0,0106 |
-0,0922 |
-0,0321 |
|
-0,1119 |
-0,0036 |
-0,124 |
0,07668 |
-0,0174 |
-0,0129 |
-0,0821 |
-0,0388 |
|
-0,0943 |
-0,0045 |
-0,1431 |
0,07337 |
-0,0148 |
-0,0146 |
-0,0722 |
-0,044 |
|
-0,0771 |
-0,0053 |
-0,1587 |
0,06783 |
-0,0122 |
-0,016 |
-0,0623 |
-0,0479 |
|
-0,0604 |
-0,0059 |
-0,1712 |
0,06143 |
-0,0096 |
-0,017 |
-0,0523 |
-0,0509 |
|
-0,0443 |
-0,0063 |
-0,1806 |
0,05312 |
-0,0071 |
-0,0177 |
-0,042 |
-0,0531 |
|
-0,0288 |
-0,0067 |
-0,1872 |
0,04455 |
-0,0046 |
-0,0182 |
-0,0314 |
-0,0546 |
|
-0,0135 |
-0,0068 |
-0,1913 |
-0,0134 |
-0,0022 |
-0,0185 |
-0,0202 |
-0,0554 |
|
0,0015 |
0,0069 |
0,1917 |
0,02484 |
-0,0002 |
0,01858 |
-0,0108 |
0,05577 |
|
0,01657 |
0,00681 |
0,18976 |
0,03529 |
-0,0027 |
0,01846 |
-0,0225 |
0,05547 |
|
0,03186 |
0,0066 |
0,18512 |
0,04409 |
-0,0051 |
0,01814 |
-0,0335 |
0,05454 |
|
0,04752 |
0,00624 |
0,17788 |
0,05146 |
-0,0076 |
0,01761 |
-0,044 |
0,05293 |
|
0,06371 |
0,00575 |
0,16807 |
0,0577 |
-0,0101 |
0,01682 |
-0,0542 |
0,05055 |
|
0,08048 |
0,00511 |
0,15564 |
0,06316 |
-0,0127 |
0,01575 |
-0,0642 |
0,04725 |
|
0,09781 |
0,00433 |
0,14039 |
0,06825 |
-0,0153 |
0,01432 |
-0,0742 |
0,04287 |
|
0,11549 |
0,0034 |
0,12185 |
0,07345 |
-0,018 |
0,01247 |
-0,0842 |
0,03718 |
|
0,13308 |
0,00233 |
0,09921 |
0,07926 |
-0,0206 |
0,01009 |
-0,0943 |
0,02991 |
|
0,14982 |
0,0011 |
0,07127 |
0,08614 |
-0,0231 |
0,00708 |
-0,1044 |
0,02075 |
|
0,1618 |
2,9E-05 |
0,04466 |
0,09241 |
-0,025 |
0,00414 |
-0,1123 |
0,01173 |
|
0,1645 |
-0,0003 |
0,0394 |
0,09344 |
-0,0254 |
0,00332 |
-0,1142 |
0,00881 |
|
0,17541 |
-0,0017 |
-0,004 |
0,10388 |
-0,0271 |
-0,0013 |
-0,1228 |
-0,0049 |
|
0,18036 |
-0,0033 |
-0,0594 |
0,11404 |
-0,028 |
-0,0067 |
-0,129 |
-0,0206 |
|
0,17686 |
-0,0048 |
-0,1212 |
0,12299 |
-0,0276 |
-0,0128 |
-0,131 |
-0,0388 |
|
0,16255 |
-0,0063 |
-0,1893 |
0,12787 |
-0,0255 |
-0,0193 |
-0,1265 |
-0,058 |
|
0,13592 |
-0,0076 |
-0,2573 |
0,12485 |
-0,0215 |
-0,0256 |
-0,1131 |
-0,0767 |
|
0,09709 |
-0,0087 |
-0,3157 |
0,11011 |
-0,0154 |
-0,0309 |
-0,0894 |
-0,0925 |
|
0,04844 |
-0,0093 |
-0,3557 |
-0,0072 |
-0,0077 |
-0,0344 |
-0,0556 |
-0,1027 |
|
-0,0055 |
0,00952 |
0,36516 |
0,04881 |
-0,0009 |
0,03542 |
-0,0226 |
0,10637 |
|
-0,0588 |
0,00923 |
0,34658 |
0,08411 |
-0,0094 |
0,03385 |
-0,0629 |
0,10182 |
|
-0,1058 |
0,0085 |
0,30286 |
0,10742 |
-0,0168 |
0,02996 |
-0,0949 |
0,09014 |
|
-0,1423 |
0,00739 |
0,24285 |
0,11898 |
-0,0225 |
0,02441 |
-0,1166 |
0,07334 |
|
-0,1664 |
0,00602 |
0,17637 |
0,12115 |
-0,0261 |
0,01803 |
-0,1281 |
0,05397 |
|
-0,1784 |
0,00451 |
0,11145 |
0,11718 |
-0,0278 |
0,01157 |
-0,1312 |
0,03436 |
|
-0,18 |
0,00295 |
0,05297 |
0,11007 |
-0,0279 |
0,00556 |
-0,1281 |
0,01616 |
|
-0,1736 |
0,00142 |
0,00294 |
0,10205 |
-0,0268 |
0,00029 |
-0,1213 |
0,0003 |
|
-0,1618 |
-3E-05 |
-0,0414 |
0,09357 |
-0,025 |
-0,0041 |
-0,1123 |
-0,0124 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.