3.4 Построение планов скоростей и ускорений.
3.4.1. Определение аналогов скоростей исследуемого станка графическим методом.
Построим план скоростей для положения ![]() . Так как аналоги скоростей не зависят
от закона изменения обобщенной координаты, принимаем
. Так как аналоги скоростей не зависят
от закона изменения обобщенной координаты, принимаем ![]() .
.
План скоростей механизма строим в следующем порядке:
1) находим скорость точки A, которая является общей для звеньев 1,2,и3
А1 €кривошипу, А2 €камню, А3 €кулисе
![]() ;
(3.28)
;
(3.28)
2) из полюса плана скоростей Pv откладываем отрезок Pva1=100мм, изображающий вектор скорости точки A (приложение, лист 2).
3) подсчитываем масштабный коэффициент скоростей:
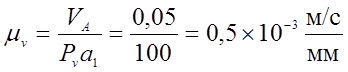 ; (3.29)
; (3.29)
4) Для определения скорости точки А2 раскладываем плоскопараллельное движение звена 2 на переносное (вращательное) вместе с точкой A3 и относительное (поступательное) по отношению к точке A3.
. Поэтому 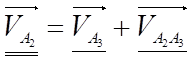 (3.30)
(3.30)
Из (3.30) выводим 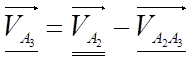 (3.31)
(3.31)
Уравнение (3.31) решаем графически. Через точку a1 проводим линию, параллельную O2B, а через полюс Pv – линию, перпендикулярную O2B.,
до их пересечения в точке a3. Векторы ![]() и
и
![]() изображают искомые векторы
изображают искомые векторы ![]() и
и ![]() (план
скоростей см. приложение, лист 2).
(план
скоростей см. приложение, лист 2).
5) Скорость точки В определяем, используя теорему подобия
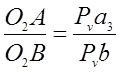 ,
вектор
,
вектор ![]() изображает искомый вектор
изображает искомый вектор ![]() ;
;
6) Скорость точки С
находим как сумму поступательной скорости звена СB и
вращательной вокруг точки B: ![]() (3,32)
(3,32)
7) Уравнение (3.32) решаем графически.
Через точку bпроводим
линию, перпендикулярную CB до пересечения с
горизонталью, проходящей через полюс Pv в точке С. Векторы![]() и
и ![]() изображают
искомые векторы
изображают
искомые векторы ![]() и
и ![]() (план
скоростей см. приложение, лист 2).
(план
скоростей см. приложение, лист 2).
8) Положения точек ![]() и
и ![]() на
плане скоростей находим, воспользовавшись теоремой подобия:
на
плане скоростей находим, воспользовавшись теоремой подобия:
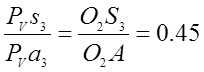 и
и 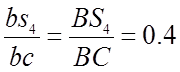 (3,33)
(3,33)
Векторы ![]() и
и ![]() изображают скорости
изображают скорости ![]() и
и ![]() .
.
9) Из плана скоростей находим:
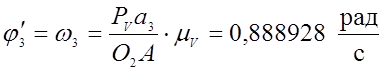 ;
(3,34)
;
(3,34)
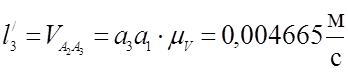 ;
(3,35)
;
(3,35)
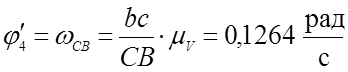 ;
(3,36)
;
(3,36)
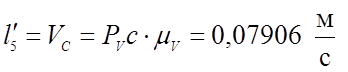 ;
(3,37)
;
(3,37)
;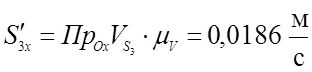 ;
(3,38)
;
(3,38)
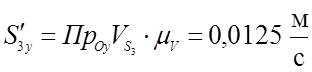 ;
(3,39)
;
(3,39)
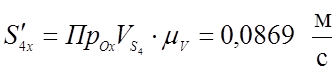 ;
(3,40)
;
(3,40)
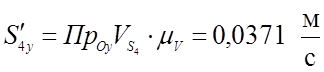 .
(3,41)
.
(3,41)
В таблице (3.7) приведены значения аналогов скоростей, полученные графическим и аналитическим методами.
Т а б л и ц а (3.7)
Результаты расчетов аналогов скоростей
|
Велич. |
|
|
|
|
|
|
|
|
|
Графич. |
0,888928 |
0,004665 |
0,1264 |
0,07906 |
0,0186 |
0,0125 |
0,0869 |
0,0371 |
|
Аналит. |
0,8823 |
0,00446 |
0,1203 |
0,07908 |
-0,0183 |
0,0123 |
-0,0858 |
0,03795 |
|
|
0,75 |
4,5 |
5,1 |
0,025 |
1,6 |
1,6 |
0,81 |
2,2 |
3.4.2. Определение аналогов ускорений исследуемого станка графическим методом.
(план ускорений исследуемого механизма см. приложение лист 3)
Задачу
решаем путем построения плана ускорений, считая ![]() постоянной величиной:
постоянной величиной:
Определяем ускорение точки A1. Полное ускорение точки A1 равно
нормальной составляющей ![]() , которая
направлена по линии АO1, к центру O1.
, которая
направлена по линии АO1, к центру O1.
![]() (3,42)
(3,42)
Из π-полюса плана ускорений – откладываем вектор, изображающий ускорение точки A1.
Подсчитываем масштабный коэффициент ускорений:
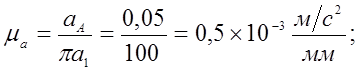 (3,43)
(3,43)
Для определения ускорения точки A3, записываем векторные уравнения:
![]() (3,44)
(3,44)
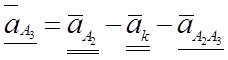 (3,45)
(3,45)
Нормальные ускорения вычисляем по формулам:
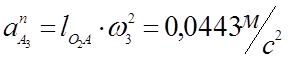 (3,46)
(3,46)
Из π- полюса план ускорений откладываем вектор πbn параллельно О2В
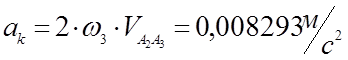 (3,47)
(3,47)
К точке а1 прикладываем вектор ка1 перпендикулярно
к О2А, затем из точки к откладываем
вектор а3к параллельно
О2А. Вектор πа3 изображает
ускорение точки А3. 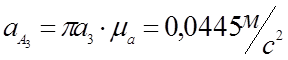 (3,48)
(3,48)
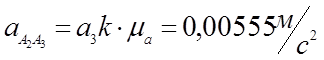 (3,49)
(3,49)
Для определения ускорения точки B звена 3 используем теорему подобия:
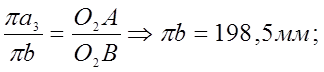 (3,50)
(3,50)
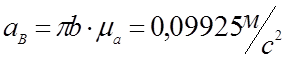 (3,51)
(3,51)
Ускорение точки С находим из уравнения: ![]() (3,52)
(3,52)
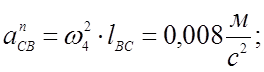
Строим вектор bcbn, изображающий нормальную составляющую аСВ параллельно BC. Уравнение (3,52) решаем графически: через точку cbn проводим линию, перпендикулярно ВС до пересечения с горизонталью, проведенной через полюс- π, в точке с Вектор πс изображает вектор ас
Из плана ускорений находим:
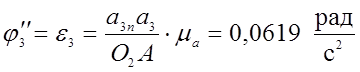 ;
(3,53)
;
(3,53)
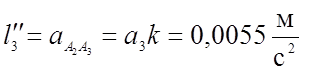 (3,54)
(3,54)
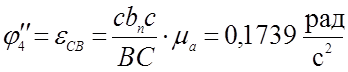 ; (3,55)
; (3,55)
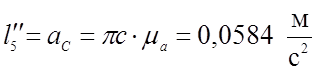 ; (3,56)
; (3,56)
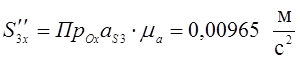 ;
(3,57)
;
(3,57)
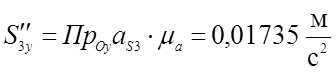 ;
(3,58)
;
(3,58)
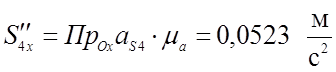 ;
(3,59)
;
(3,59)
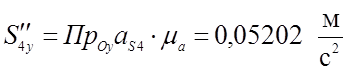 .
(3,60)
.
(3,60)
Результаты расчета аналогов ускорений
Т а б л и ц а 3.8.
|
Велич. |
|
|
|
|
|
|
|
|
|
Графич. |
0,0619 |
0,00555 |
0,1739 |
0,0584 |
0,00965 |
0,01735 |
0,0523 |
0,05202 |
|
Аналит. |
-0,0604 |
-0,0059 |
-0,1712 |
0,06028 |
-0,0096 |
-0,017 |
-0,0523 |
0,0509 |
|
|
2,5 |
5,9 |
1,64 |
2,88 |
0,52 |
2,1 |
0 |
2,2 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.