Министерство общего образования Российской Федерации
Тольяттинский государственный университет
Кафедра «Машиноведения и инженерной экологии»
КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛАНЕТАРНЫХ И
ДИФФЕРЕНЦИАЛЬНЫХ МЕХАНИЗМОВ
Методические указания к лабораторной работе №10 по курсу ТММ
Тольятти
2005 г.
ЦЕЛЬ РАБОТЫ
Изучить кинематику планетарных и дифференциальных механизмов и определить их передаточные отношения теоретическим и практическим методами.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
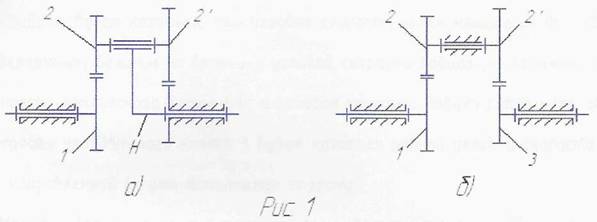
Отличительной особенностью планетарных и дифференциальных механизмов является наличие б их составе зубчатых колёс с подвижными осями. На рис. 1а изображена схема механизма, у которого колесо 3 неподвижно, а звено Н, называемое водилом, вращается. Колёса 2 и 2' представляют собой единый блок, т.е. это одно звено. Этот блок вместе с водилом Н вращается вокруг оси центрального колеса I, называемого солнечным. Колёса 2 и 2', совершающие сложное движение, называются сателлитами. Такой механизм называется планетарным по аналогии с солнечной системой.
Степень подвижности таких механизмов определяется по формуле Чебышева, и для механизма, представленного на рис 1а,
W=3n-2P5-P4=3x3-2x3-2=1
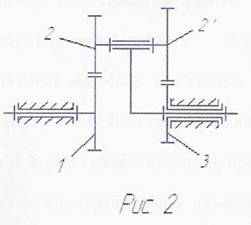
Если в этом механизме колесу 3 предоставить свободу вращения (рис.2), то степень подвижности механизма изменится:
W=3n-2P5-P4=3x4-2x4-2=2
Полученный результат говорит о том, что для определения законов движения всех звеньев этого механизма, называемого дифференциальным, должно быть два следующих звена. У планетарного механизма должно быть одно ведущее звено, так как роль второго звена, закон движения которого задан, играет неподвижное коле со 3.
Для определения передаточного отношения планетарных механизмов применяется известный из механики метод обращения движения (метод инверсии).
Будем рассматривать движение всех колёс относительно водила. Наблюдателю, располагающемуся на водиле, будет казаться, что угловые скорости колем меньше их действительных (абсолютных) величин на величину угловой скорости водила (на величину угловой скорости переносного вращения), а угловая скорость водила равна нулю. Угловая скорость неподвижного колеса 3 будет казаться равной угловой скорости водила, но направленной б противоположную сторону.
Метод инверсии состоит в том, что всем звеньям механизма (в том числе и неподвижному) сообщается угловая скорость, равная и противоположная угловой скорости водила. Таким образом, метод инверсии в данном случае эквивалентен остановке водила и освобождению неподвижного колеса. Относительное движение колёс по отношению друг к другу и к водилу при этом, конечно, не изменяется.
Механизм, полученной в результате инверсии, представляет собой зубчатую передачу с неподвижными осями, передаточное отношение которой легко определяется. На рис 16 представлена кинематическая схема обращённого механизма, полученная б результате инверсии из планетарного механизма (рис.1а). Вычитая из угловых скоростей колёс угловую скорость водила, получаем их угловые скорости в относительном вращении по отношению к водилу, или угловые скорости колёс обращенного механизма:
ω1Н=ω1-ωН; ω2H=ω2-ωH; ω3Н=ω3-ωН=-ωН
Определяя передаточное отношение обращённого механизма, получаем
U13(Н)= ω1Н / ω3Н=( ω1-ωН)/ (-ωН)=1-( ω1-ωН)=1- U13(Н)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.