Экономика и менеджмент \ Управление эксплуатационной работой и качеством перевозок

Основные принципы управления эксплуатационной работой железных дорог (Глава 3 учебного пособия по курсу «Управление эксплуатационной работой железных дорог и качеством перевозок»), страница 7

Если обозначить поток за период времени tкак N(t), средняя интенсивность потока в принятую единицу   времени    (час,   сутки):    .

Поскольку интенсивность потока - величина переменная (рис. 3.1), изменяющаяся под воздействием множества факторов, необходимо знать распределение интенсивностей при известной средней интенсивности r{t) или известном математическом ожидании М [r(t)].

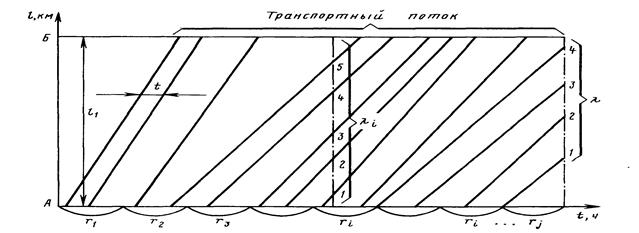
Рис. 3.1. Зависимость транспортного потока от его характеристик rи

Транспортный поток однозначно определен, если известны (t) или М[r(t)], а также вид распределения (закон распределения) интенсивностей и характеристики этого закона. Итак, интенсивность-поток, поступающий в единицу времени. В качестве единицы времени можно принимать временные отрезки 0,25, 05, 0,75, 1,0 ч или 2, 3, 4 ч или большие по длительности отрезки времени.

Если обозначить переменную интенсивность транспортного потока через х, часовую интенсивность r, то плотность распределения интенсивностей транспортного потока в течение времени Т можно выразить Законом Гаусса, условно допуская непрерывность х:

1        _*-*■>' /(*) =

, где  - среднее квадратическое отклонение интенсивности транспортного потока за время Т.

Интегральная  форма  этого  закона

,

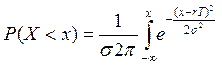Следует понимать, что нормальный закон согласуется со статистическими данными при значениях Т>  0,75... 1,5 ч. В меньших периодах времени по критериям согласия часто подходит закон Пуассона:

,

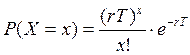При любых значениях периода T наилучшее согласование со статистическими данными, как правило, получается у биномиального закона, вероятность прибытия х поездов за время Т для которого определяется

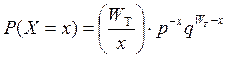, где WТ - максимально возможный подвод поездов (число возможных ниток графика) за время Т; р- вероятность того, что по какой-то нитке графика прибудет поезд, определяется отношением расчетного числа поездов к максимально возможному: ; q- вероятность обратного   события;   q = 1 — р;   - число сочетаний из WT элементов по х, равное:

.

Возможность использования трех законов для аппроксимации статистических данных имеет свое обоснование в теории вероятностей, из которой следует, что и нормальный, и пуассоновский законы являются аппроксимирующими для биномиального, причем первый при , второй - при и .

В эксплуатации железных дорог используются и другие законы распределения (при разработке технологии станций для аппроксимации транспортного потока часто применяются распределения Эрланга, гамма-распределение и др.).

Поток поездов, таким образом, однозначно определяется распределением интенсивности r{t). Кроме того, потоки поездов (составов) характеризуются также дисперсией D(rTi) или D(J) (при задании потока распределением интервалов между поездами), среднеквадратическим отклонением , коэффициентом вариации , коэффициентом асимметрии, коэффициентом эксцесса и другими параметрами распределения. Следовательно, поток поездов (составов) характеризуется набором параметров:

i = 1, 2, ... , п;      j = 1, 2, ... , к.

Изменение   параметров   потока под воздействием таких операций, как прием поездов на станцию, их обработка, расформирование, образование новых составов (в сортировочном парке), окончание формирования, подготовка к отправлению, отправление, т.е. под воздействием фаз обслуживания потока, будем называть трансформацией потока. Если поток прошел через к фаз, то с   потоком   произошла   к-кратная трансформация. В выражении (3.1) число трансформаций обозначается индексом j. Трансформация потока может приводить к существенным изменениям его параметров. Положив для исходного потока j=0 и обозначив трансформацию потока на фазе его обработки , последовательность видоизменений параметров потока можно записать в виде:

Скачать файл