Численные методы решения обыкновенных дифференциальных уравнений и систем: Методические указания к курсовой работе, страница 9

  2.20   0.04027   1.09112

  2.40   0.24752   0.94850

  2.60   0.40765   0.62859

  2.80   0.49137   0.19662

  3.00   0.48399  -0.26917

  3.20   0.38680  -0.68841

  3.40   0.21694  -0.98392

  3.60   0.00574  -1.09433

  3.80  -0.20654  -0.99462

  4.00  -0.37940  -0.70748

  4.20  -0.48090  -0.29291

  4.40  -0.49312   0.17230

  4.60  -0.41394   0.60782

  4.80  -0.25725   0.93517

  5.00  -0.05166   1.08806

  5.20   0.16383   1.03227

  5.40   0.34796   0.78059

  5.60   0.46644   0.38686

  5.80   0.49814  -0.07421

  6.00   0.43758  -0.52249

  6.20   0.29532  -0.87864

  6.40   0.09708  -1.07239

  6.60  -0.11975  -1.06106

____________________________

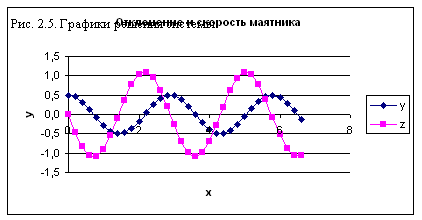
Графики функций y(x), z(x) показаны на рис.2.5.

2.3.  Модель типа "хищник - жертва” ( пример решения системы дифференциальных уравнений первого порядка

2.3.1 Постановка задачи и ее математическая модель

Рассмотрим динамику популяции двух видов, взаимодействующих между собой по типу "хищник - жертва". При этом предполагается, что жертва может найти достаточно пищи для пропитания, но при каждой встрече с хищником последний убивает жертву. Примеры таких видовых взаимоотношений дают волки и кролики, паразиты и некоторые организмы, на которых они паразитируют. Требуется исследовать изменение во времени популяций жертв и хищников

Обозначим через  ,  соответственно, количество жертв и хищников в момент времени  t. Предположим, что скорость роста числа жертв пропорциональна их количеству (при условии, что имеется достаточное количество корма), с положительным коэффициентом прироста популяции (коэффициент рождаемости минус коэффициент смертности)  и  числу встреч хищников с жертвами, т.е. произведению    c некоторым отрицательным коэффициентом  ,  т.к. при встрече число жертв уменьшается.  Тогда популяция жертв подчиняется следующему дифференциальному уравнению

               

Для популяции хищников изменение численности популяции происходит из-за  естественной убыли при отсутствии пищи, пропорциональной количеству хищников, и  роста количества пищи, пропорционального  количеству встреч жертв с хищниками, что ведет к уравнению:

               

 Таким образом, мы получили систему нелинейных дифференциальных уравнений

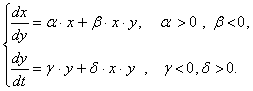                                                          (2.13)

Зададим начальные условия при  t=0

                                                                                (2.14)

Она является частным случаем системы (1.10)-(1.11). 

2.3.2 Расчетные формулы

Составим программу на Паскале для решения задачи общего вида (1.10)-(1.11) методом Рунге-Кутта четвертого порядка. Следовательно, нужно взять в качестве расчетных формул формулы  (1.12)-(1.13), приведенные выше. Отметим, что в данной задаче обозначения отличны от обозначений задачи общего вида. Поэтому следует положить:

t=x, x=y, y=z.

Исходные данные

Начальное и конечное значение аргумента  a,b.

Начальные значения неизвестных функций  .

Число отрезков разбиения области интегрирования  n

Параметры системы   .