Численные методы решения обыкновенных дифференциальных уравнений и систем: Методические указания к курсовой работе, страница 12

Изменяя параметры поведения популяций можно получить совершенно другой вариант решения, например, катастрофический, при котором один вид исчезает полностью, а  второй вид становится очень малочисленным (см. рис 2.8).

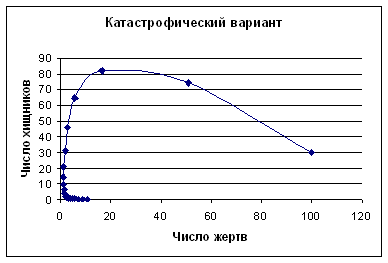
Рис. 2.8.. Траектория решения при

Замечания.

1.  При большом числе шагов результаты расчетов рекомендуется выводить в файл.

2.  Приведенный пример расчетов можно использовать в качестве контрольного варианта.

3.  Можно рассматривать взаимодействие видов другого типа, например, взаимопомощь видов или конкуренцию.

3. Задания к курсовой работе.

3.1. Уравнения первого порядка

Решить численно указанную задачу Коши для уравнения первого порядка

1) методами Эйлера и Рунге -Кутта, используя табличный процессор Excel

2) методом Рунге-Кутта, с помощью программы на языке Турбо Паскаль 7.0.

3) построить графики решений в Excel, с помощью Мастера диаграмм

4) провести анализ полученных результатов

Номер задачи	Уравнение	Отрезок [a, b]  изменения аргумента	Начальное условие- y(a)	Шаг h
1		[0,1]	y(0)=1	0.1
2		[0,2]	y(0)=0.65	0.2
3		[0,1]	y(0)=0.5	0.1
4		[0,2]	y(0)=0.5	0.2
5		[0,1]	y(0)=0.5	0.1
6		[1,2]	y(1)=0.5	0.1
7		[1,2]	y(1)=1	0.1
8		[1,2]	y(1)=0.5	0.1
9		[1,2]	y(1)=0.5	0.1
10		[1,2]	y(1)=0.6	0.1
11		[1,2]	y(1)=0	0.1
12		[1,2]	y(1)=0	0.1
13		[1,2]	y(1)=0	0.1
14		[1,2]	y(1)=0	0.1
15		[1,2]	y(1)=0	0.1
16		[1,2]	y(1)=0	0.1
17		[1,2]	y(1)=0.5	0.1
18		[0,1]	y(0)=0	0.1
19		[1,2]	y(1)=0	0.1
20		[1,2]	y(1)=0	0.1