где x - произвольная точка струны, находящейся в покое и задаваемой отрезком прямой, t - время, u=u(x,t) - отклонение струны от ее положения в покое, a - коэффициент, связанный со свойствами струны
5. Процесс распространения тепла в стержне или в плоской области произвольной формы описывается уравнениями теплопроводности:
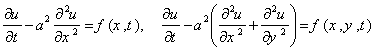 , (5)
, (5)
где x, y - координаты точки тела, t - время, u - температура. Функция в правой части уравнений не равна нулю, если в теле имеются источники тепла. Аналогично, описывается распространение тепла в трехмерном теле или процесс диффузии вещества в некотором объеме.
6. Если процесс распространения тепла или диффузии вещества является установившимся, т.е. распределение температуры или концентрации не зависит от времени, то оно подчиняется уравнению Пуассона:
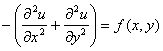 .
(6)
.
(6)
![]() При нулевой правой части получим
уравнение Лапласа:
При нулевой правой части получим
уравнение Лапласа:
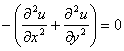 . (7)
. (7)
В последних трех примерах не рассматривались граничные и начальные условия. Корректные постановки задач с начальными, граничными или начально-краевыми условиями изучаются в соответствующих разделах высшей математики.
Из курса высшей математики хорошо известны линейные дифференциальные уравнения с постоянными коэффициентами, для которых легко находится аналитическое решение. К таким уравнениям относятся примеры (1)-(2). Уравнение (3) - нелинейное уравнение второго порядка и его решение не может быть получено простым интегрированием. При решении обыкновенных дифференциальных уравнений часто возникает необходимость использования приближенных методов, т. к. большинство практических задач не имеет аналитического решения. Уравнения в частных производными, как правило, могут быть решены также только численными методами.
Приближенные методы существенно расширяют круг задач, для которых можно найти решение, и являются мощным инструментом моделирования реальных явлений.
В данном пособии рассматривается один из важных методов решения задачи Коши для обыкновенных дифференциальных уравнений и систем - метод Рунге-Кутта. В качестве простейшего вида метода Рунге-Кутта дан пример решения уравнения методом Эйлера. Рассмотрены примеры решения уравнений первого и второго порядка и системы уравнений первого порядка, причем, проведено качественное исследование поведения решения, даны варианты заданий для курсового проектирования..
Для выполнения расчетов рекомендуется использовать табличный процессор MS Excel, а также систему программирования Турбо Паскаль, что позволяет дублировать вычисления. В случае выполнения расчетов с помощью одного средства необходимо рассчитывать контрольный вариант. При решении задачи на компьютере следует придерживаться общепринятой последовательности шагов:
1. Постановка задачи
2. Математическая модель задачи
3. Выбор численного метода решения, написание расчетных формул
4. Разработка алгоритма, представление его в виде блок-схемы, определение структуры данных
5. Расчет контрольного варианта
6. Отладка программы.
7. Выполнение расчетов
8. Анализ результатов
После проведения расчетов нужно оформить отчет к курсовой работе в виде пояснительной записки. Правила оформления пояснительной записки являются стандартными для всех дисциплин и могут быть получены в УКЦ.
Затем следует подготовиться к защите работы. Для успешной защиты необходимо общее знакомство с численными методами решения прикладных задач, понимание основных методов решения дифференциальных уравнений, описанных ниже, и обоснование проведенных расчетов, а также анализ полученных результатов.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.